3. 9. 5. 1. 1. Устный счёт

«Устный счёт. В народной школе С. А. Рачинского» — картина русского художника Н. П. Богданова-Бельского (1868—1945), написанная в 1895 году.
На классной доске написан пример, который ученикам необходимо решить:

На картине изображена деревенская школа конца XIX века во время урока арифметики при решении дроби в уме. Учитель — реальный человек, Сергей Александрович Рачинский (1833—1902), ботаник и математик, профессор Московского университета. На волне народничества в 1872 году Рачинский вернулся в родное село Татево, где создал школу с общежитием для крестьянских детей, разработал уникальную методику обучения устному счёту, прививая деревенским ребятишкам его навыки и основы математического мышления. Эпизоду из жизни школы с творческой атмосферой, царившей на уроках, и посвятил своё произведение Богданов-Бельский, сам в прошлом ученик Рачинского.

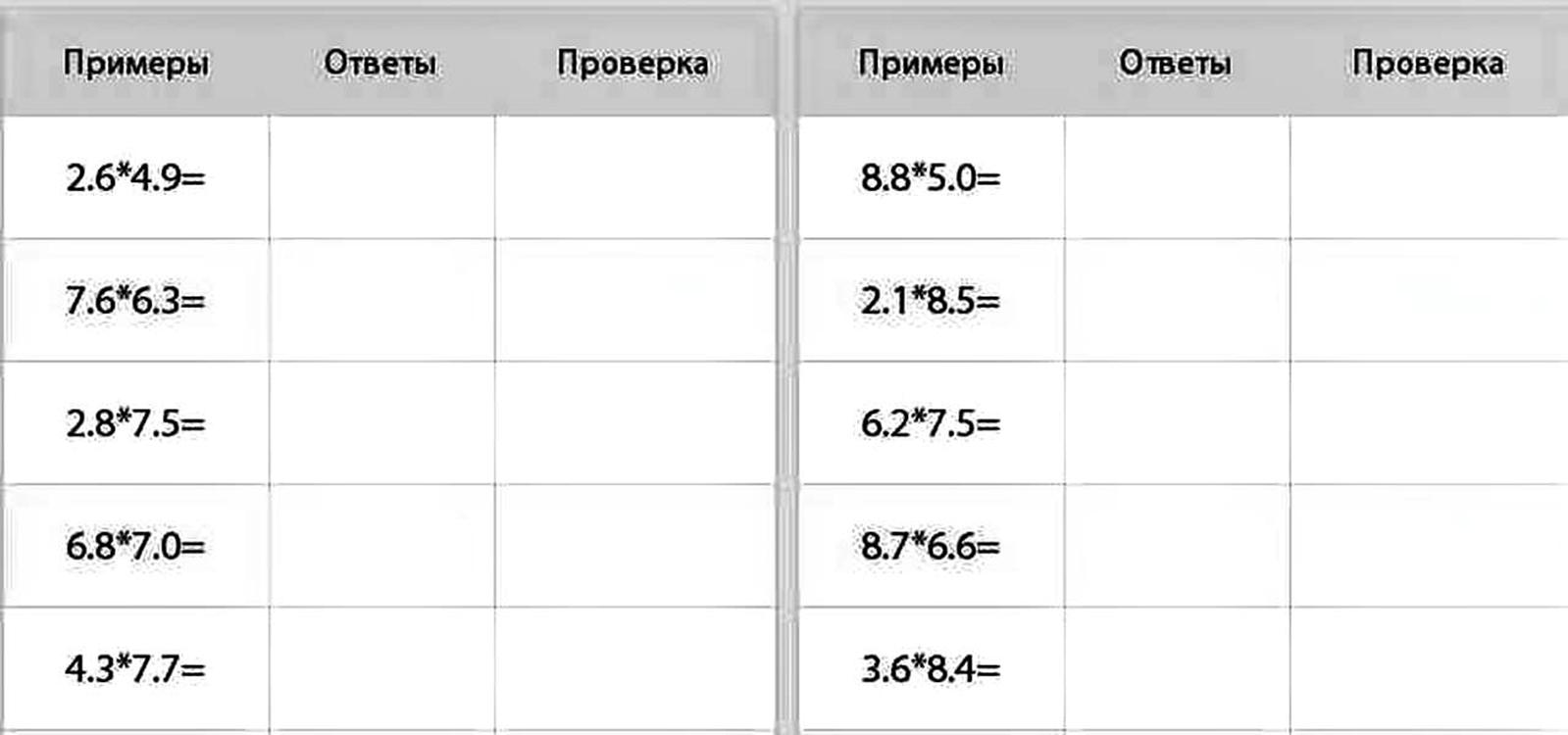
Ниже приведен скриншот современного задания в 2016 году в 11 классе на экзамене ЕГЭ, для так сказать детей в возрасте 17 лет.

Для пояснения сути можете проследить ход мыслей тех учеников для решения первой задачи с картины Богданова-Бельского и сравнить с тем, а как бы вы подошли к решению этого примера.

Исходим из того, что решать надо в уме, а пример для детей 11-12 лет. Значит это должно быть целое число. Берем, и складывает числитель (делаем прикидку) по минимуму 100+100+100+100+100=500. Но число должно быть больше. В знаменателе 365, тогда в числителе большой вероятностью может быть 730. Значит, ответ равен = 2.
Решение вероятное, но может быть с ошибкой.
Тогда проверка №1, при условии, что знакомы с квадратами этих чисел и держим в уме два числовых параметра:
100+121+144=365, 13^2+14^2=365. ДВА раза по 365. Ответ те самые, которые ДВА.
Тогда проверка №2, при условии, что можем держать в уме три числовых параметра
10*10+11*10+11+12*10+12*2=365 13*10+13*3=169 14*10+14*4=196 169+196=365 . . . . И опять ДВА раза по 365.
Тогда проверка №3, при условии, что можем держать в уме три числовых параметра, и знаем ФОРМУЛУ СУММЫ КВАДРАТОВ. . .
И так далее… Если вы поняли о чём речь, тогда вы не глупее тех детей на картинке.

Что даёт устный счёт человеку по жизни:

Лучше проходит любое обучение в независимости от вида деятельности.
Приучается всё делать точно, замечать детали, приучает к экономии и порядку.
Помогает предвидеть будущее, просчитывать несколько ходов вперёд по любой теме.
Помогает создавать новые образы предметов и явлений, соединять их именно в мозаичную структуру.
Повышает общее внимание и умение концентрироваться.
Сопутствует к правильному словесному выражению мыслей в точном и сжатом виде.

Человек, освоивший быстрый устный счёт, как правило, начинает намного быстрее и правильнее мыслить.

Не надо стремиться к решению примеров с большими дробями и многозначностью. Наша задача не выступать шутами со сцены и всех удивлять своими успехами и умениями. Всё должно быть в меру. Особенно это касается детей, родители которых калечат их, радуясь, когда ребенок в уме начинает решать громадные примеры. По большому счёту это всё отклонения, ведущие к шизофрении и к «хорошему», это всё не приведёт. Всё должно развиваться ровно и равномерно.

Нам необходимо натренировать устный счёт хотя бы до базового уровня счёта самых сложных примеров в форме двузначного вида и начальные варианты трёхзначных примеров.

Существует несколько приёмов для упрощения устного счёта, приведём лишь несколько, дабы был понятен смысл. Более полную информацию сможете легко найти по соответствующему запросу в сети Интернет.

Сложение.

Чтобы научиться в уме, складывать числа, нужно уметь банально на автомате складывать числа до 10. Любая сложная задача приводится к решению нескольких простых действий.

Чаще всего ошибки и заминки возникают при сложении чисел с переходом через число 10. При сложении и при вычитании хорошо применять технику «опоры на десяток». Мы сначала мысленно представляем, сколько одному из слагаемых, не достаёт до 10, а потом приплюсовываем к 10 оставшуюся до второго слагаемого разность.

Допустим, сложим числа 8 и 6. Чтобы из 8 вышло 10, не хватает 2. Затем к 10 останется прибавить 4=6-2. В конечном счете, получаем: 8+6=(8+2)+4=10+4=14

Основное умение в сложении больших чисел – разбить их на разрядные части, а потом соединить эти части между собой.

Допустим нам нужно сложить два числа: 356 и 728. Число 356 можно представить в виде 300+50+6. То же самое, 728 будет выглядеть как 700+20+8. Теперь соединяем:

356+728=(300+700)+(50+20)+(8+6)=1000+70+14=1084

Вычитание.

В отличие от сложения, при вычитании надо «разбить» только то число, которое мы отнимаем.

Сколько будет 528-321. Разбиваем число 321 на разрядные части и у нас выходит: 321=300+20+1.

Теперь вычисляем: 528-300-20-1=228-20-1=208-1=207

Теперь необходимо эти процессы представить визуально в своём воображении. Всех нас учили считать в столбик, то бишь двигаться сверху вниз. Наша задача научиться считать не сверху вниз, а слева направо, разбивая числа на разрядные части.

Умножение чисел в уме.

Умножение – это многократное повторение числа. Если надо умножить 8 на 4, то это то, что число 8 необходимо повторить 4 раза.

8*4=8+8+8+8=32

Если наша задача все сложные задачи свести к более простым, то тогда нам нужно уметь умножать все однозначные числа. Для этого есть хороший инструмент и её название - таблица умножения. Эту таблицу необходимо выучить до автоматизма, и так чтобы вы могли её образно представить в своём воображении целиком одной картинкой, и только потом браться за тренировку устного счета.

Таблица умножения.

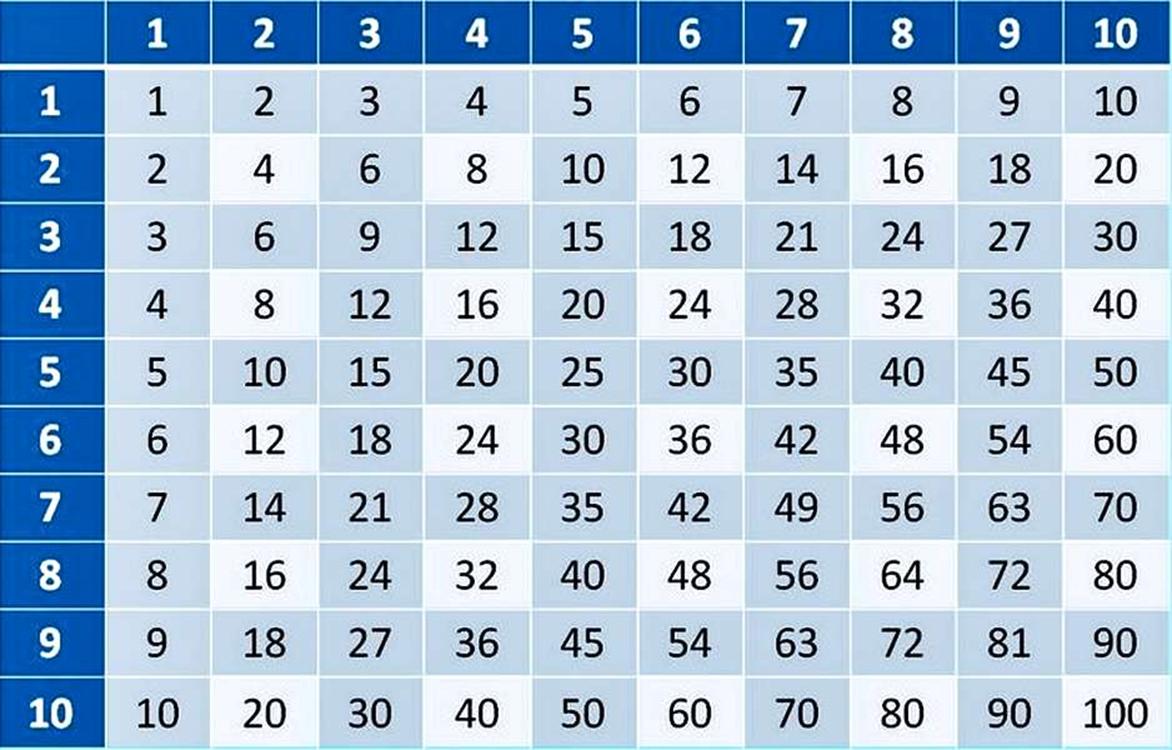
Умножение многозначных чисел на однозначные.

Сначала работаем с умножением многозначных чисел на однозначные числа. Допустим, нам надо умножить число 528 на число 6. Разбиваем 528 на разряды и движемся от старшего числа к младшему. В начале умножаем, а затем складываем то что получается.

528=500+20+8

528*6=500*6+20*6+8*6=3000+120+48=3168

Умножение двузначных чисел

В этом случае увеличивается нагрузка на нашу краткосрочную память. И если идёт некая заминка значит, нам необходимо пройти дополнительный тренинг на развитие памяти.

Умножаем число 28 на число 32. Для этого упрощаем всю операцию к умножению на однозначные числа. Разбиваем число 32 на 30+2

28*32=28*30+28*2=20*30+8*30+20*2+8*2=600+240+40+16=896

Для понимания приведём ещё один вариант. Умножим между собой числа 79 и 57. Здесь нам необходимо взять число «79» 57 раз. Разложим нашу задачу на части. В начале умножим число79 на число 50, а затем уже – 79 на 7.

• 79*50=(70+9)*50=3500+450=3950

• 79*7=(70+9)*7=490+63=553

• 3950+553=4503

Умножение на 11

Крутая хитрость с числом 11. Чтобы умножить двузначное число на 11, две цифры числа складываем, друг с другом, и получившуюся сумму вписываем между цифрами исходного числа. Получившееся в результате трехзначное число, это и есть результат умножения.

Для проверки умножим число 54 на 11.

• 5+4=9

• 54*11=594

Возведение в квадрат

С помощью другого приема, можно очень легко и быстро возводить двузначные числа в квадрат, которые завершаются на 5. Результат начинается с произведения первой цифры числа, на следующую цифру идущую за ней по возрастанию. Получатся, что если эту цифру обозначить через n, то следующей за ней по иерархии цифрой будет n+1. Результат заканчивается на квадрат последней цифры, то есть квадрат 5.

Пример. Возведем в квадрат число 75.

• 7*8=56

• 5*5=25

• 75*75=5625

Деление чисел в уме

По сути, это операция, обратная умножению. С делением чисел до 100 никаких проблем вообще возникать не должно. Существует таблица умножения.

Деление на однозначное число

При делении многозначных чисел на однозначное число необходимо выделить максимально большую часть, которую можно разделить с помощью таблицы умножения.

Допустим, есть число 6144, которое необходимо разделить на 8. Из таблицы умножения совершенно ясно, что на 8 будет делиться число 5600. Имеем:

6144:8=(5600+544):8=700+544:8

Далее из числа 544 также выделяем максимально большое число, которое делится на 8. Имеем:

544:8=(480+64):8=60+64:8

Осталось разделить 64 на 8 и получить результат, сложив все результаты деления

64:8=8

6144:8=700+60+8=768

Деление на двузначное число

В этом случае необходимо работать с правилом последней цифры результата при умножении двух чисел.

При умножении двух многозначных чисел последняя цифра результата умножения всегда совпадает с последней цифрой результата умножения последних цифр, этих чисел.

К примеру, умножим число 1325 на число 656. По правилу, последняя цифра в получившемся числе будет 0, так как 5*6=30. Действительно, 1325*656=869200.

Теперь, зная эту информацию, рассмотрим деление на двузначное число.

Разделим числа 4424:56

Вначале будем использовать метод «подгона» и найдем пределы, в которых лежит наш результат. Нам необходимо найти число, которое при умножении на 56 даст 4424. Интуитивно попробуем число 80.

56*80=4480

Значит, искомое число меньше 80 и явно больше 70. Определим его последнюю цифру. Её произведение на 6 должно заканчиваться цифрой 4. Согласно нашей таблице умножения, нам подходят результаты 4 и 9. Логично предположить, что результатом деления может быть либо число 74, либо 79. Делаем проверку:

79*56=4424 (Всё верно).

Если бы не подошло число 79, второй вариант обязательно оказался бы правильным.

Самый главный совет это постепенность и ежедневность.

То есть, необходимо тренироваться каждый день. Не переживайте и не расстраивайтесь если в начале не будет быстрого результата. Результат обязательно будет. А нам быстро и не надо, все, что делается постепенно и медленно, то всё это оседает крепко и надолго.

Большой помощью в наших тренировках могут оказать современные приложения и программы для компьютера и телефона. В сети Интернет присутствует множество таких помощников – так что выбирайте, устанавливайте и тренируйтесь

Приведу лишь то, что мне попалось сразу с первого поискового запроса.

Интернет:

Тренажер устного счёта на телефон.

http://www. sposobnostiuma. com/trenazher-ustnogo-scheta/

На Google Play можно найти приложение под название Математические хитрости и ещё очень много по запросу – тренируем устный счёт.

Ещё раз. Именно устный счёт создаёт особые алгоритмы в вашем подсознании, это по сути особы подпрограммы которые потом будут на автомате не только считать числа, но и участвовать в других мыслительных операциях, в том числе и чувственных и интуитивных. По сути, вы поднимите общий свой уровень вашего интеллекта, и самое главное ваше подсознание будет работать на более сложном программном обеспечении. То есть, любое дело, абсолютно любое, которое вы будете делать, будет делаться быстрее и лучше чем у того индивида который с трудом может в уме что-либо сложить или разделить.

См. видео:

3126_Знания для элиты, а для быдла простая школа/

/873_Математика_Уроки Шалвы Амонашвили/

/874_Математика Приемы быстрого счета/

Следующая страница ➤

Данилёнок Вадим Евгеньевич
С этого места Вы можете бесплатно скачать книгу по материалам сайта и выразить благодарность автору по указанной ссылке
СКАЧАТЬ КНИГУ БЕСПЛАТНО
или нажав на верхнюю картинку

* * * * * * * * *