7. 2. 3. Статистика и вероятность

Лучше сказать, Статистика и Теория Вероятности

См. словарь:

/10. 3. 8. Вероятность и вероятностная предопределенность/

Статистика — это отрасль знаний, наука, в которой излагаются общие вопросы сбора, измерения, мониторинга, анализа массовых статистических (количественных или качественных) данных и их сравнение; изучение количественной стороны массовых общественных явлений в числовой форме.

Теория Вероятности - это раздел математики, изучающий случайные события, случайные величины, их свойства и операции над ними.

Сама по себе вероятность описывает повторяемость каждого из различимых частных вариантов множественных, вероятностно предопределённых явлений одного и того же класса. А вероятность выбранного частного варианта есть мера этой повторяемости, и может быть найдена как отношение числа благоприятных для данного варианта элементарных исходов к общему числу элементарных исходов в данном испытании

Статистикой и Теорией Вероятности необходимо овладеть в обязательном порядке и это необходимо для того, чтобы научиться принимать взвешенные решения. Ведь зная статистические данные и анализируя закономерности, можно, по сути «предсказать» исход события.

Суть в том, что теория вероятности в обязательном порядке нужна для реализации успешного управления. Именно через определение необходимой статистики и выборки в надлежащих количествах можно спланировать необходимые действия, оценить факторы среды которые давят, контролировать через математически точное определение количества точек контроля, их частоту и сложность.

Допустим, в неком городе мэра поддерживает ровно 60% населения. Сколько человек надо опросить, чтобы результат попал от 58% до 62% с вероятностью 99,9%?

Человек, знакомый с теорией вероятности, назовет точную цифру – 25. 5 тысячи человек.

То есть, если всё это не знать и не учитывать, то можно очень легко ошибиться в своих прогнозах, а значит и в надлежащем управлении.

Любая информация в единичном виде и тем более без учета вероятности её появления, в том числе и единожды приобретенный опыт по любому вопросу, являются одними из главных причин при принятии ошибочного решения.

Человек неосознанно постоянно находится под влиянием информации единичного характера. К примеру, ваш сосед обожает некого поставщика услуг Интернета, и вы тоже подключаетесь к этому оператору. Вашему другу не повезло с автомобилем определенной марки, с тех пор вы даже не хотите попробовать сесть за руль такой машины. Ваш родственник знал человека, который погиб в автомобильной аварии, потому что, тот оказался зажат ремнём безопасности и поэтому он никогда не пристёгивается и это так же на вас влияет.

Такого вида информационного давления, на нас обрушивается превеликое множество, оно просто льётся из СМИ, и особенно из Интернета и социальных сетей.

Да, существуют простые и мало влияющие как на вас, так и на других людей решения, которые вы принимаете под напором выше указанного.

Но существуют более важные решения. Именно эти решения необходимо принимать исходя из реальных статистических показателей и вероятностных данных. И эти показатели, и данные должны быть получены в ходе хорошо спланированных и тщательно проведенных работ.

И именно в ракурсе управления по любым направлениям, необходимо об этом постоянно помнить и самое главное, надо иметь соответствующие знания и личный навык проводить такие работы, хотя бы в упрощенном виде.

Поэтому, если вы управленец любой категории, то вы должны не позволять единичной информации оказывать на вас однозначно управляющего влияния.

При этом лучше всего опираться на статистическую информацию, основанную на больших случайных выборках, которая представляет целевую совокупность, а не просто отдельную ситуацию.

Теория вероятности и математическая статистика это обязательный атрибут для полноценного управления. К примеру, вам надо из двух направлений чего-либо, выбрать одно единственное направление. В этом случае, имея навык выше упоминаемого, управленец должен собрать все необходимые начальные данные и условия о двух вариантах. Далее он должен просчитать вероятность удачного разрешения для каждого варианта, и уже после этого, имея на руках вероятность реализации либо в процентах, либо в десятичных дробях, принять решение в сторону того, у которого вероятность реализации больше другого.

Изначально здесь очень важную роль играет сбор начальных параметров, которые так же могут быть просчитаны как вероятности.

К примеру, два направления, каждый в отдельности просчитывается по вероятности возможности быстрого приобретения необходимых запчастей или по вероятность их поломки из прошлого опыта. Так же можно, к примеру, учитывать вероятность утери, проблем доставки, сложности реализации и так далее. То есть, составляется некий перечень однородных вероятностей по каждому направлению, они суммируются, и в итоге получаем общие вероятности и потом их уже сравниваем.

Управленец, который свободно не владеет этим всем, шарлатан и вредитель.

Осваивание и достижение необходимого уровня по указанным вопросам, на начальном этапе, достигается через банальное множественное решение стандартных задач по теории вероятности с последующим практическим применением в реальной жизни.

Именно множественное решение задач и нарабатывает необходимый алгоритм в подсознании, и последующий навык до уровня автоматизма, при решении любой проблемы, где есть двойной расклад начальной информации. По сути, имея такой автоматизм, человек впоследствии при любой проблеме будет получать на уровень сознания через эмоцию, некое требование к реализации процесса выявления как главных, так и зависимых вероятностей по каждому сравниваемому направлению и необходимому общему решению при окончательном выборе.

По большому счёту не имея начальных навыков по Теории Вероятности и Математической Статистики нет возможностей полноценно при ПФУ определять и отслеживать основные контрольные, управляемые и свободные параметры. Именно через F(x) и f(x), через математическое ожидание, медиану, дисперсию, отклонение, и так далее можно выйти именно на, те параметры, без которых удачное управление просто невозможно.

Самым простым способом применения теории вероятности и статистики является практика выявления лучшего варианта, при выборе из двух возможных которые даются при разрешении любых жизненных ситуаций.

Суть в том, что именно простой расчёт вероятности возможного события, который может быть более 51 процента всегда даёт весомые преимущества, особенно если речь идёт относительно событий на длительных интервалах. То есть, если надо в процессе управления из двух вариантов выбрать единственный, то именно законы вероятности нам в помощью. При этом, как при работе с выборкой на длительных интервалах и, особенно на коротких интервалах и малой выборке, в обязательном порядке необходимо задействовать натренированное чувство Меры.

Теперь для самого начала предоставим совсем немного вводной информации для вхождения в тему, но самое главное это прохождение всех уроков, ссылки на которые будут даны в завершении этого документа.

Случайная величина – величина, которая может принимать то или иное численное значение из заранее определенного множества, притом заранее неизвестно, каково именно это значение. Задать случайную величину – значит:

задать значения, которые она может принимать;
задать, каковы вероятности появления различных значений случайной величины.

Случайная величина бывает дискретной и непрерывной

Примеры дискретных случайных величин: оценка успеваемости студента, число попаданий в мишень, группа инвалидности, степень тяжести заболевания и др.

Примеры дискретных случайных величин: измерение температуры тела градусником, спортивный результат в беге или прыжках, рост и масса тела человека, сила мышц и др.

Теперь немного поподробнее.

Начнём с простого примера для дискретной случайной величины.

Был некий экзамен в некой группе. На выходе мы получили некий набор статистик, которые разместим в таблице.

В первой строке это все возможные оценки – от единицы (кол) до пятерки.

Во второй строке соответственно количество таких полученных оценок. То есть, к примеру, мы видим, что тройку получили 10 человек.

В третьей и последующих строках вероятность получения той или иной оценки в разных представлениях.

Если человек ничего не имеет представления о теории вероятности, то всё что он может сделать с этими данными, так это просчитать среднюю оценку по группе и всё.

1+2*3+3*10+4*8+5*2 = 79

1+3+10+8+2 = 24

Средняя оценка будет равна 79/24 = 3,291. Это, по сути, аналогично тому, когда рассчитывают среднюю зарплату по стране. Или когда складывают тех, кто есть мясо с теми с теми, кто ест капусту и говорят, что все едят голубцы. Информация о среднем, не говорит о том, в каких соотношениях находятся исследуемые данные, а значит нельзя отследить их динамику изменений. Именно так у нас ни чиновники, ни депутаты не знакомые с теорией вероятности и статистикой не видят и не могут видеть, что год от года процент очень богатых паразитов увеличивается, а всё остальное население становится всё беднее и нищебродствуют. Но при этом наблюдается рост средней зарплаты по стране.

Нас естественно это всё не устраивает, и поэтому мы продолжим.

Таб. 7. 2. 3. -1

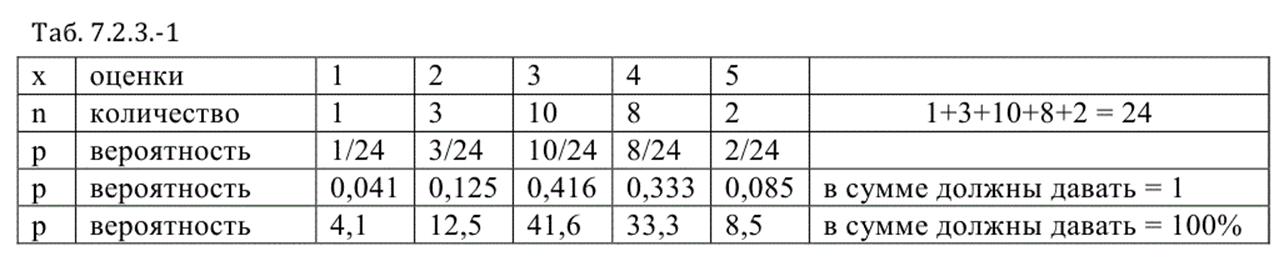
Вероятность, какого либо события – это численное выражение возможности его наступления.

Вероятность появления соответствующей оценки считается очень легко и это видно из таблицы. Суммируется всё количество оценок и потом через отношение с соответствующей оценкой ( n ) находится значение ( p ).

Полученная выше таблица это уже информация о распределении случайной величины под названием, – «Сколько и каких оценок получили студенты».

По сути это уже – Закон распределения случайной величины.

Это всё можно представить графически через полигон дискретной случайной величины:

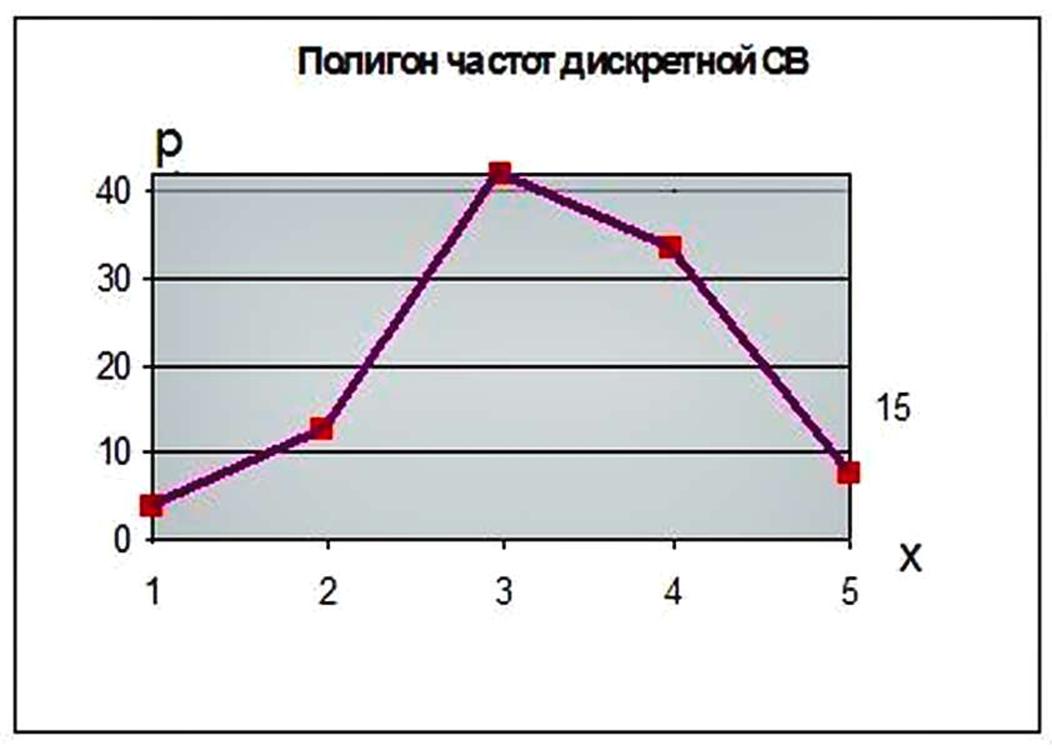
То есть, мы заранее не знали, какие будут оценки и в каком количестве, но после экзамена мы получили некую информационную картину, некую зависимость как всё распределилось. По сути, мы имеем некий информационный ряд, который характеризует случайную величину под названием «сколько и каких оценок получили студенты».

А если есть выявленные зависимости, то естественно можно найти и функцию этих зависимостей.

Каждая случайная величина полностью определяется своей функцией распределения, т. е. является ее “паспортом” и содержит всю информация об этой величине. Поэтому изучение случайной величины заключается в исследовании ее функции распределения, которую часто называют просто распределением.

Функция распределения случайной величины, в нашем случае функция распределения случайной величины под названием «сколько и каких оценок получили студенты», находится довольно просто. Нам необходимо в нарастающем режиме к « n » прибавлять значение « х ».

Таб. 7. 2. 3. -2

В результате имеем Функцию распределения дискретной случайной величины F(x).

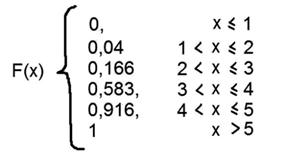
Эта функция графически будет выгладить так:

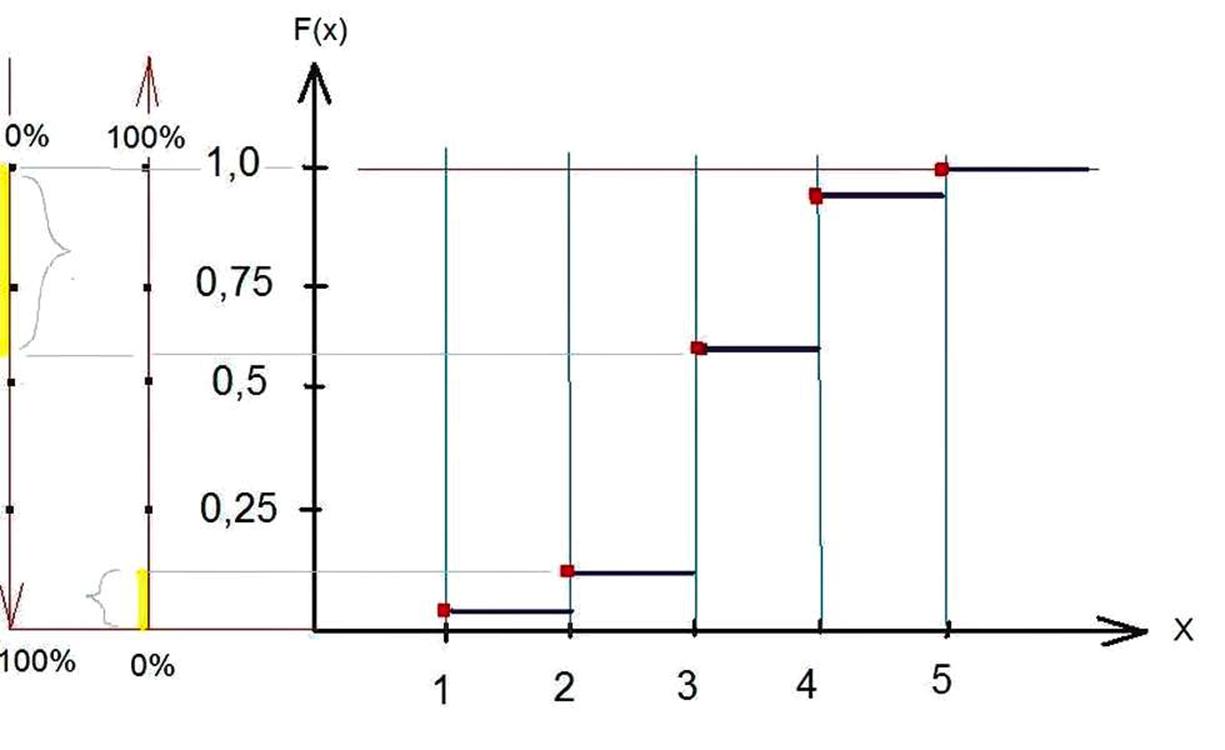
Вся изюминка графического такого представления нашего случайного распределения в том, что мы можем сразу видеть, допустим, в процентах, сколько и каких оценок получила группа.

Можно по отдельности, а можно в разных вариантах. К примеру, жёлтым цветом выделено на дополнительных осях что, к примеру, 5 и 4 группа имеет около 41 % процента от всех оценок, а 1 и 2 получило 16 %.

И если, к примеру, провести точно такой же расчёт за несколько лет, и расположить графики рядом, то можно выявить тенденцию увеличения или уменьшения тех групп учеников, которые были взяты за контрольные группы. По сути, можно по выбранным контрольным группам, или параметрам, сразу и наглядно видеть процесс получения знаний и, следовательно, уровень компетентности и качество управления тем или иным органом и конкретными отвечающими за это управленцами. То есть, можно очень легко и быстро оценить, как происходит управление процессом, который нас интересует.

Отслеживать и сравнивать изменения разных данных от наблюдаемых процессов управления можно ещё и исходя из сопоставления изменений математически высчитываемых основных параметров в виде числовых характеристик случайных величин. То есть, к примеру, если мы делаем периодически некие выборки контрольных параметров некого процесса. То в последствии сравнивая их динамику изменений и математически высчитывая числовые характеристики, мы можем аналитически выявлять те ситуации, когда необходимо в той или иной мере воздействовать на управляемые параметры в нашем движении к достижению цели.

Перечислим основные такие величины.

Математическое ожидание, мода, дисперсия, среднее отклонение, коэффициент вариации.

1. Математическое ожидание.

По сути математическое ожидание М(х) это среднее значение. Оно характеризует среднее значение случайной величины (ожидаемое значание)

Математическое ожидание случайной величины (СВ), равно сумме всех ее возможных значений, умноженных на вероятности этих значений.

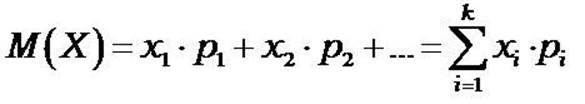
2. Мода.

Мода (M*) – характеризует значение случайной величины, реализующееся с наибольшей вероятностью. По сути здесь всё просто берём найденное среднее значение М(х) – в нашем случае для оценок студентов будем иметь М(х) = 3,291. к этому значению ближе всего находится оценка (n) c числовым значением 3, смотрим в нашу таблицу и тамже видим что больше всего оценок было именно троек. Следовательно, мода М* = 3

3. Дисперсия.

Дисперсия показывает степень разброса случайной величины (разброс данных) относительно Математического ожидания М(х).

Дисперсия равна сумме квадратов отклонений отдельных значений случайной величины, от ее математического ожидания, умноженных на вероятности этих значений

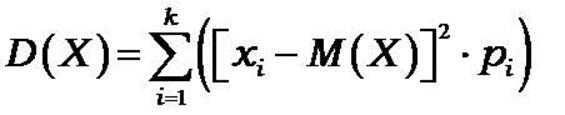
Суть в том, чтобы исходя из своего управления, добиваться уменьшения дисперсии относительно желаемых параметров, что ведёт к наилучшим показателям.

4. Среднее отклонение.

Среднее отклонение показывает на какую величину в среднем отличатся значения случайной величины от её математического ожидания М(х)

Среднее отклонение случайной величины это корень квадратный из дисперсии.

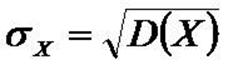
Суть в том, чтобы исходя из своего управления, добиваться уменьшения среднего отклонения, что ведёт к более точным показателям.

5. Коэффициент вариации.

Коэффициент вариации случайной величины характеризует стандартное отклонение в долях от математического ожидания.

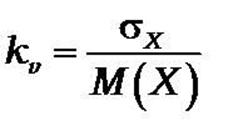
Суть в том, что низкие показатели вариации говорят, к примеру, о стабильной ситуации на производстве или в других процессах, где была произведена выборка контролируемых параметров.

Для наглядности приведём пример расчёта вышеуказанных величин.

Имеем некий закон распределения, случайных величин получения оценок на экзамене студентами. В этом примере задан другой ряд оценок, он отличается от того, который мы рассматривали ранее, так что не путаемся.

Поучается что, наблюдая, к примеру, как из года в год меняется дисперсия или другие величины при сдаче экзаменов, можно очень легко в сравнении, оценивать качество управления процессом образования. И к тому же вовремя вводить новые управляемые или контрольные параметры и анализировать действие на объект управления и на субъект управления свободных параметров, о которых мы будем подробнее рассказывать в разделе ПФУ.

Всё что говорилось выше, это всё относится к дискретным процессам, где случайная величина может принимать конечные, изолированные значения из некоторого числового промежутка.

К примеру, это, как число попаданий в мишень, бросок игрального кубика, группа инвалидности, степень тяжести заболевания, число звонков, число испытаний и так далее.

Но есть ещё и непрерывные случайные величины, которые могут принимать все значения, из некоторого числового промежутка.

К примеру, это, измерения температуры, мощности, веса, временные измерения любых процессов, по сути, все измерения которые не имеют изолированного и независимого значения.

Для этих процессов важно понять, что и как происходит между выявленными контрольными точками, что, по сути, нам и даёт дополнительную информацию о ходе управляемого процесса.

Возьмем, к примеру, процесс измерения температуры в некой группе людей. В результате измерений температур было выявлено.

То есть, было сделано 100 замеров температуры тела у 100 человек и распределение в периодах были занесены в таблицу. К примеру, было выявлено 5 человек с температурой в диапазоне от 35,5 до 36 градусов. Далее было выявлено 30 человек с температурой в диапазоне от 36 до 36,5 градусов и так далее. Затем по уже знакомой методике была вычислена вероятность ( p ).

По сути, получили закон распределения случайной непрерывной величины.

Это всё можно представить графически через полигон непрерывной случайной величины:

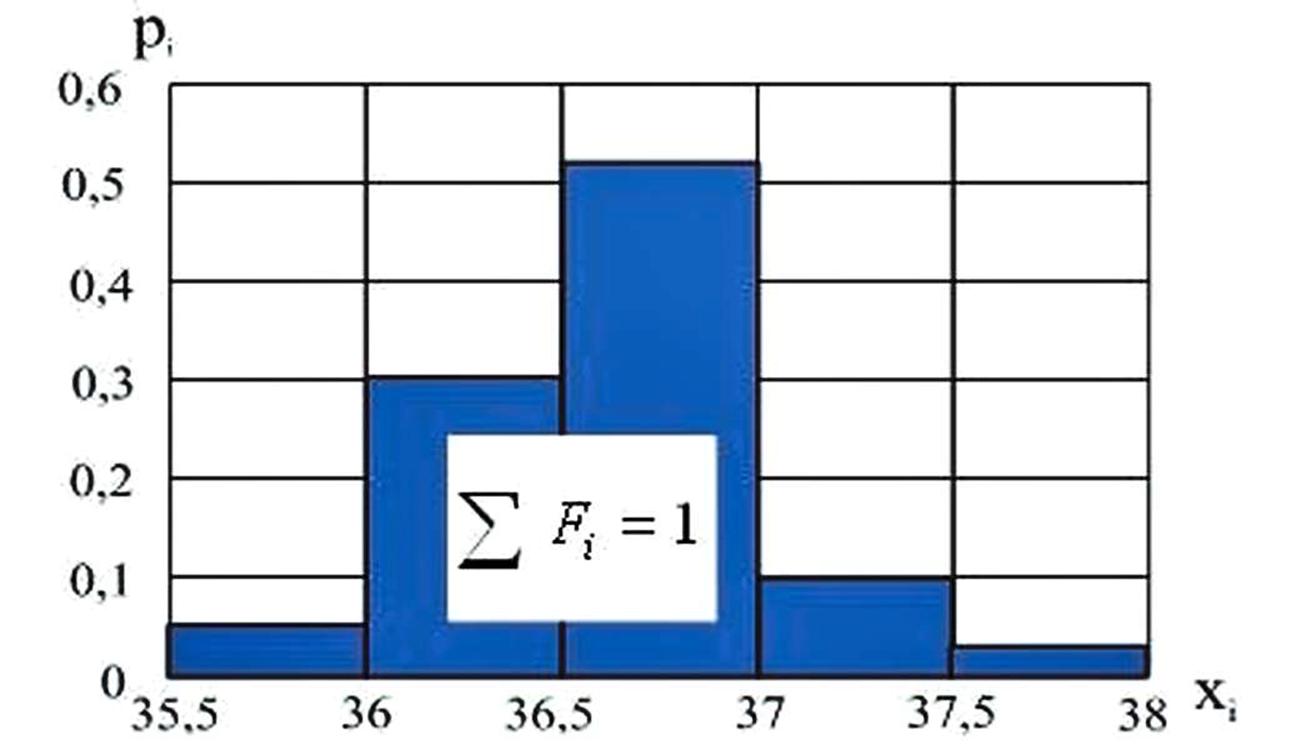
Далее рассчитываем Функцию распределения случайной непрерывной величины.

Представляем в графическом виде.

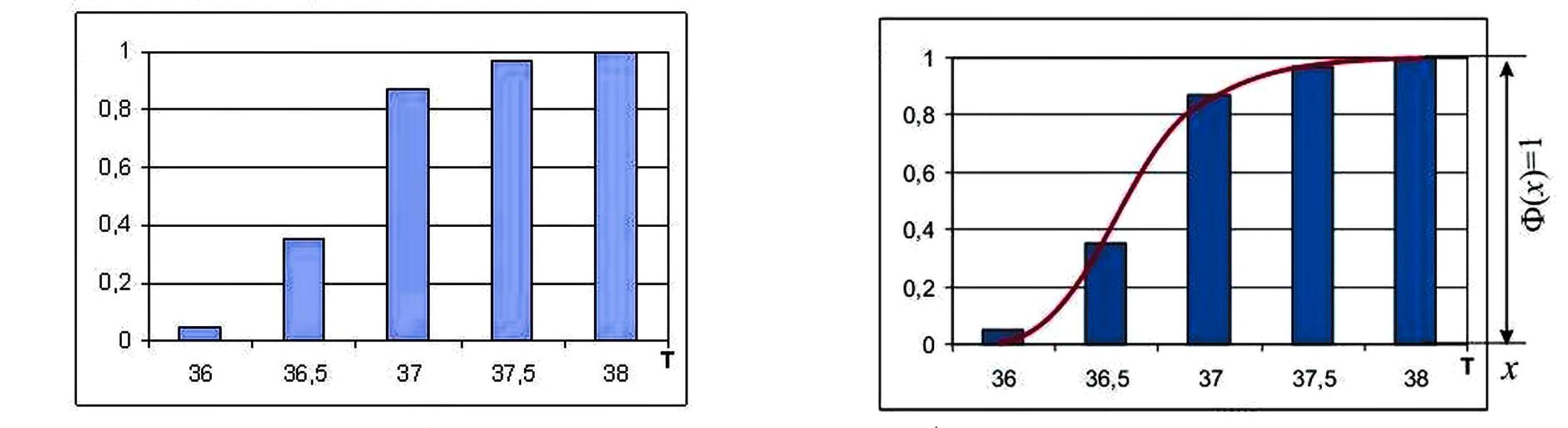
Здесь мы можем провернуть точно такой же «фокус» как и при рассмотрении графика дискретной величины. То есть, мы можем сразу видеть, допустим, в процентах, сколько и какая температура преобладает и как она может изменяться в ракурсе изменения, к примеру, управлением здоровьем. Вспомните, как мы ранее отмечали необходимые данные жёлтым цветом в новых левых осях с процентами. Здесь даже выходит лучше, так как имеем непрерывную величину, т. е. некую неразрывную кривую (правый рисунок), поэтому можем даже предположить и выбрать совсем другие диапазоны и уже их анализировать.

К примеру, вот такой вариант функции распределения случайной величины:

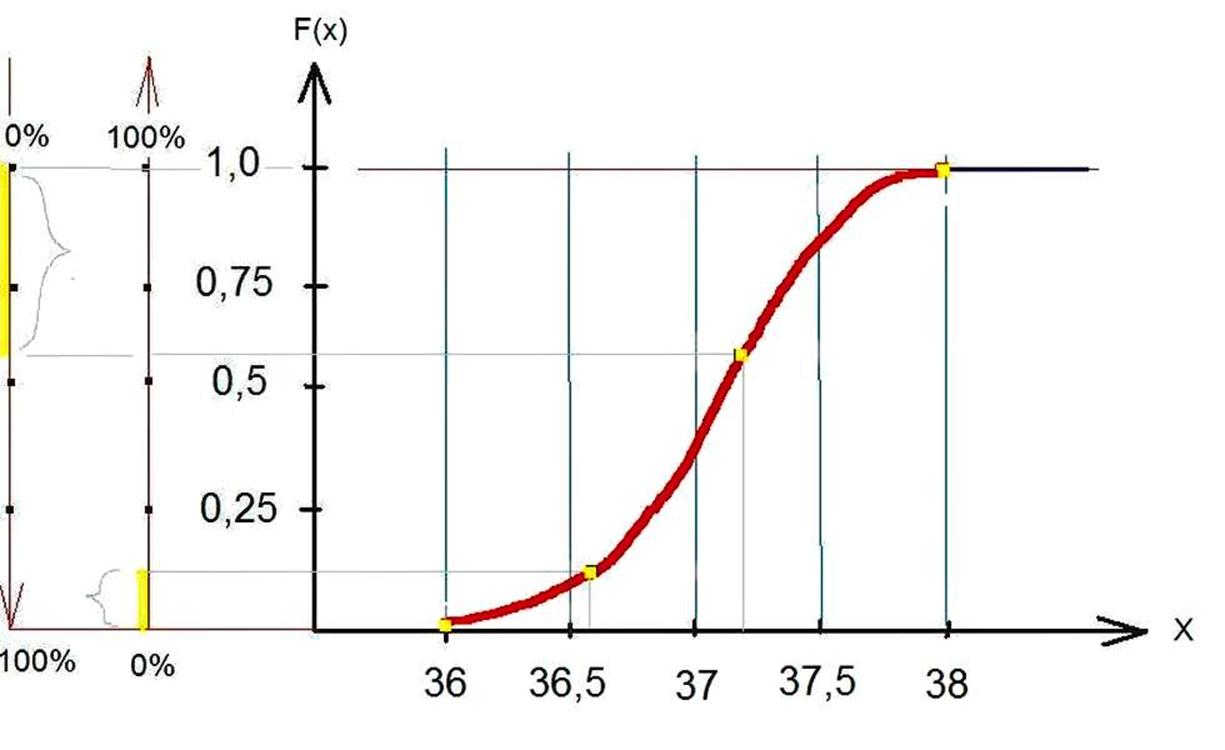
Но мы видим, что в отличие от функции дискретной случайной величины у нас на одинаковых отрезках, к примеру от 36 до 36,5 и на отрезке от 37 до 37,5 имеется разница в концентрации вероятности (если очень грубо – длина графика разная).

И возникает вопрос, как оценить эту концентрацию на различных промежутках.

Эффективный ответ на поставленный вопрос даёт функция плотности распределения вероятностей.

Сразу заметим, что для дискретной случайной величины такой функции не существует.

Имея ранее построенный полигон непрерывной случайной величины, мы его можем представить через

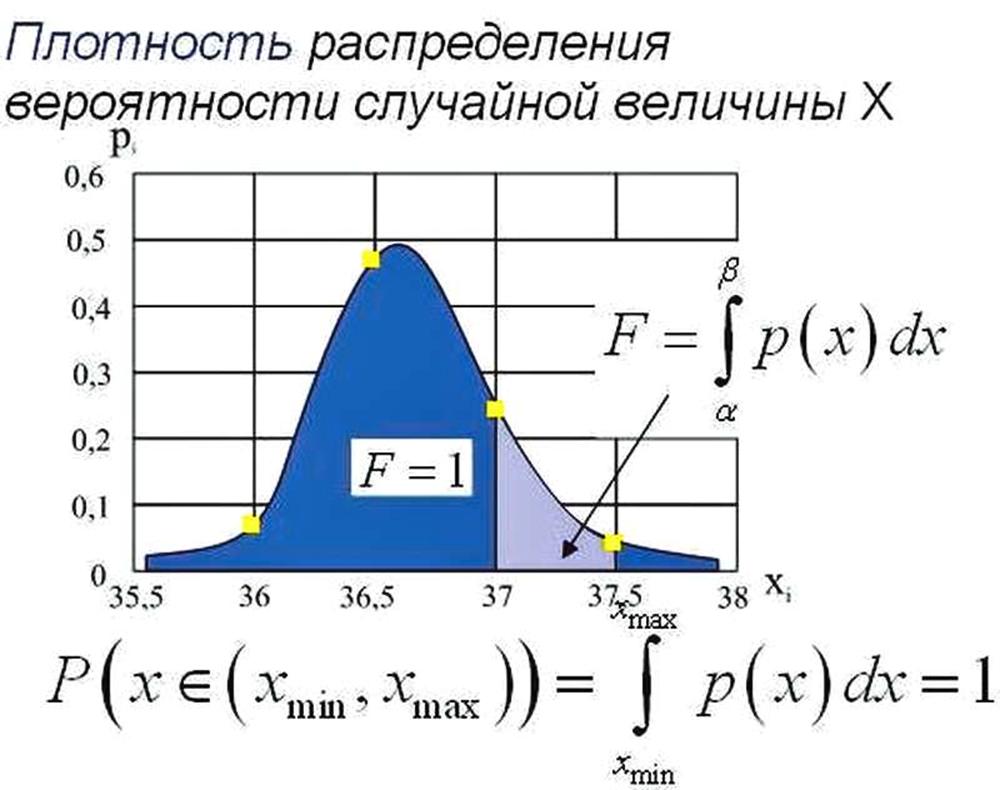
После чего уже можно выйти и на функцию плотности распределения СВ.

Функция плотности распределение случайной величины или дифференциальная функция распределения представляет собой производную функции распределения f (x) = F’(x).

Примечание.
Самое простое образное объяснение производной - это "скорость". Производная - изменение чего-то (путь) в единицу чего-то (время).
К примеру, производная от функции у=3(х) равна трём (3).
То есть, здесь скорость ровна трём (3) на каждую последующую единицу - каждый раз на три (3) больше.
По сути, имеем то, что функция у=3(х) ПРОИЗОДИТСЯ из ТРОЕК.
Есть два действия - сложение и вычитание, и есть их производные.
К примеру, умножение это производная сложения и как результат слагаемых.
По большому счёту, изменяя что-либо, получаем некую функцию изменения этого, и чтобы потом найти по функции, что и как мы изменяли, мы берём производную. Изменяя периметр, мы получали площадь, изменяя площадь, получали объём. Следовательно, производная от объёма это площадь, а производная от площади это периметр.
Надо всегда помнить, что производная это именно процесс как "скорость" изменения, поэтому это именно зависимость и в нашем случае её можно представить через площадь.

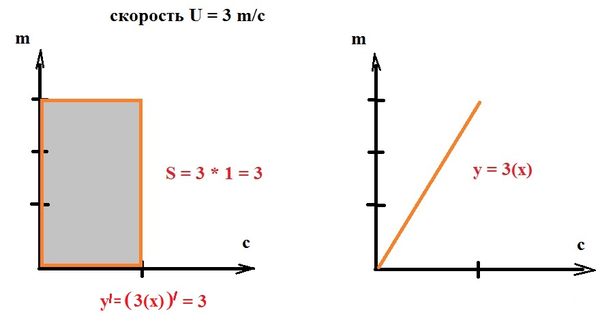
То есть, в нашем случае, надо банально брать производную от каждого куска.

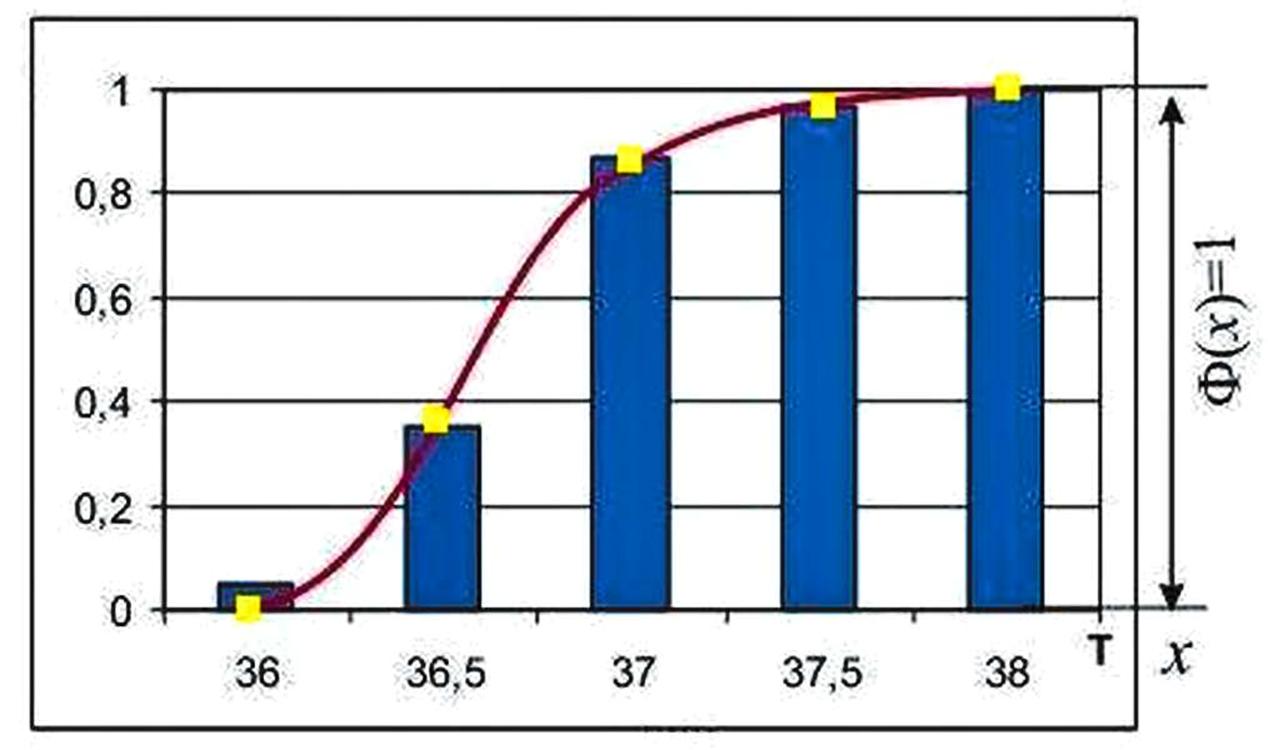
Суть непрерывной функции в том, что как ни странно она непрерывна. То есть, мы имеем непрерывный зависимый ряд, а это значит, что существуют математические зависимости, которые мы можем представить банальной формулой фикции и графиком. Допустим, у нас есть некий ряд:

Таб. 7. 2. 3. -3

Имеем явную зависимость у = х², по сути, имеем функцию f(х) = х².

В нашем примере мы тоже имеем некую зависимость, а к примеру на отрезке от 37 до 37,5 имеем некий участок как график фикции с началом 0. 87 и завершением 0,97 – эти данные берем из таблицы строка (р*).

Мы, по сути, имеем некую, грубо говоря, кривую, которая характеризует, к примеру, продолжительность некого процесса или изменение некого процесса. В нашем случае это все, что было на отрезке от 36 до 36,5.

Взяв, грубо говоря, производную это куска мы получим функцию плотности распределения. Проделав всё аналогичным образом со всеми данными температурных замеров, мы в итоге получим график функции плотности распределения СВ.

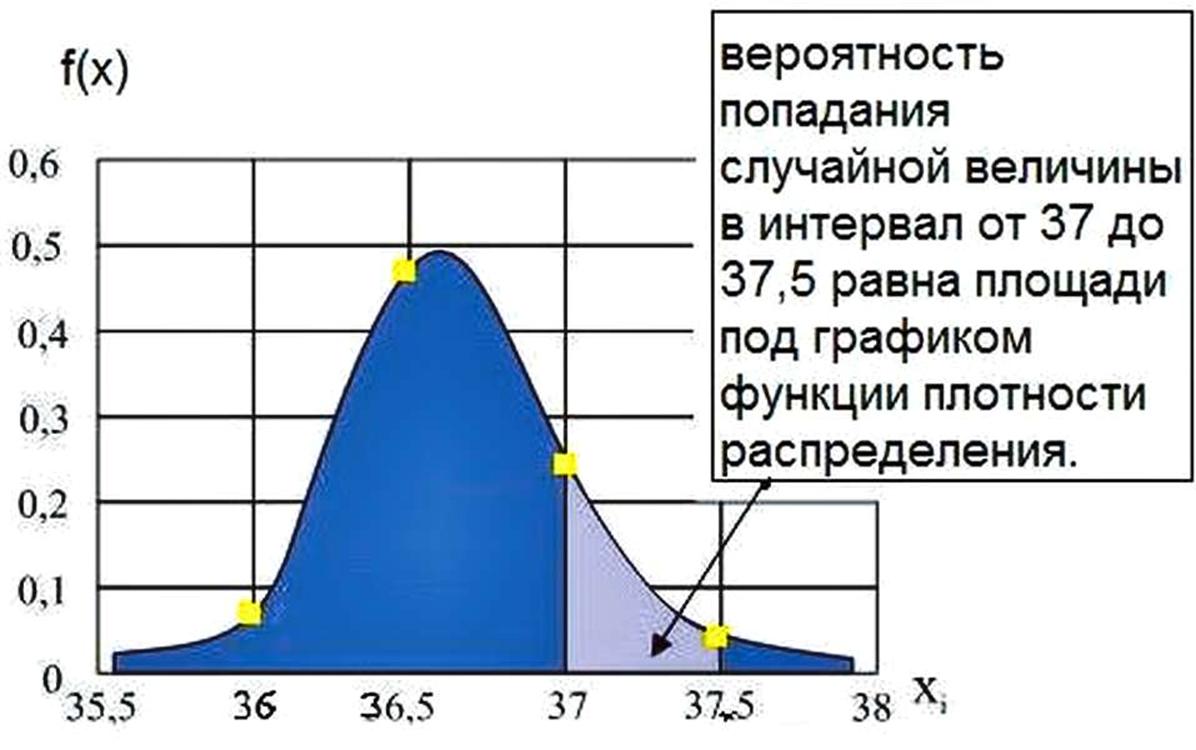
Главное понять, что суть плотности распределения заключается в том, что вероятность попадания случайной величины в интервал от 37 до 37,5 равна площади под графиком функции плотности распределения.

Вследствие этого, если мы в будущем будем делать ещё аналогичные замеры, то, сравнивая, грубо говоря, площади исследуемых интервалов мы можем в лёгкую графически так и аналитически видеть их соотношения и изменения. Что, по сути, нам и даёт необходимую информацию в качестве управления теми процессами, для которых мы выбрали эти значения как контрольные параметры. Так же очень наглядно можно сравнивать и близко лежащие площади и тенденции их изменения, а по сути перетекания неких ресурсов из одной области в другую. То есть именно увеличение площади одного интервала за счёт другого и выявляет, к примеру, ту самую нищету, о которой шла речь выше, когда вроде в среднём всё хорошо и все едят голубцы, только одни всё больше едят капусты, а другие всё больше мяса.

Если очень грубо, то вышеуказанные процесс можно наглядно представить, к примеру, в трёх графиках плотности распределения СВ.

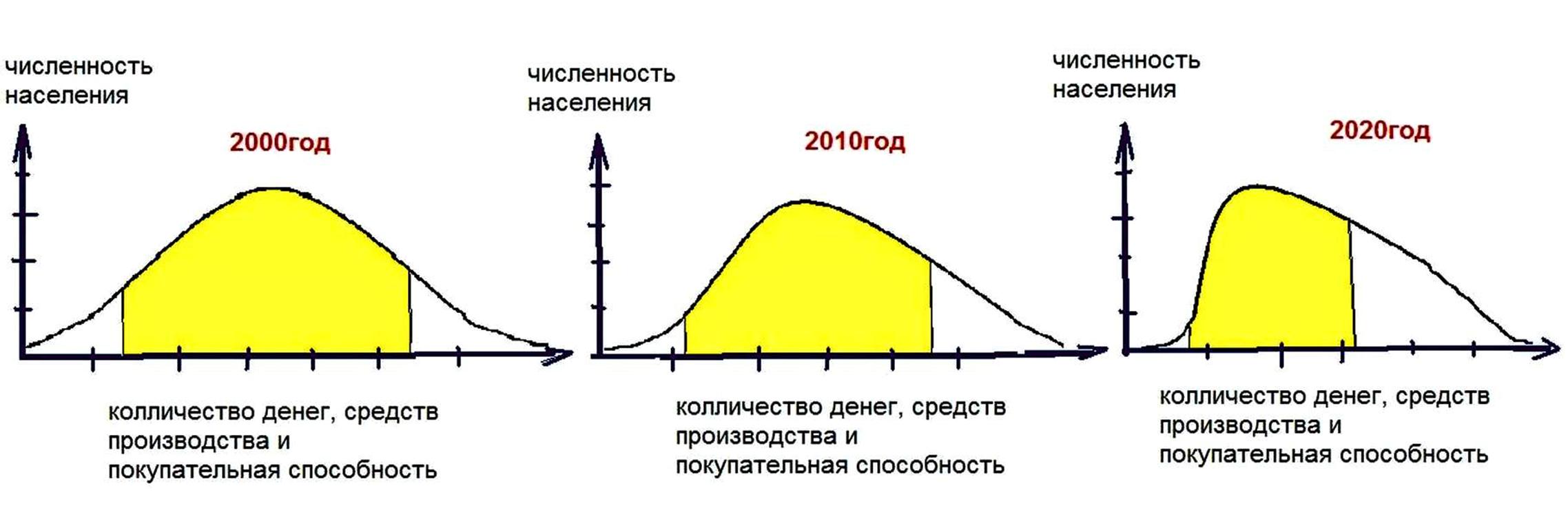
Мы видим, что плотность распределения (площадь) «людей» сдвинулась к малому количеству денег. То есть где-то 80 процентов людей стали беднее, а сверх богатых стало больше и это естественно за счёт основного населения, которое стало намного беднее, и появился преобладающий класс нищих. По сути, это очень хорошее управление, если исходить из вектора целей зажравшейся элиты.

Без понимания сути этих графиков, как раздела теории вероятности и математической статистики, не возможно легко выявить и увидеть процесс усиления несправедливости и паразитирования. А, следовательно, накопления психического напряжения неудовлетворенности у миллионов людей. Которое в обязательном порядке выльется в очередной бунт и развал государственности, как это уже было не один раз на протяжении Русской истории. А так как психодинамика общества, по сути, не изменилась, то нет никаких других способов этого избежать, если не снижать разрыв несправедливости и не двигать графики к нормальному распределению и заодно не править строй психики к «Человек» у большинства населения. Очень интересно будет увидеть, к примеру, функцию распределения плотности СВ строев психики людей от животного до строя психики «Человек» на временной шкале. Скорее всего, площадь вообще за многие века не двигается.

По большому счёту любой процесс должен стремиться к приблизительному виду первого графика из трёх выше показанных. То есть не должно быть много бедных и много богатых должно быть большинство среднего уровня и желательно симметрично.

В теории вероятности и мат. статистики были исследованы множества рядов и функций и были выявлены, некие часто используемы стандартные распределения.

Ярким примером такого распределения является так называемое нормальное распределение.

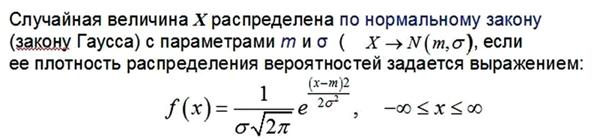
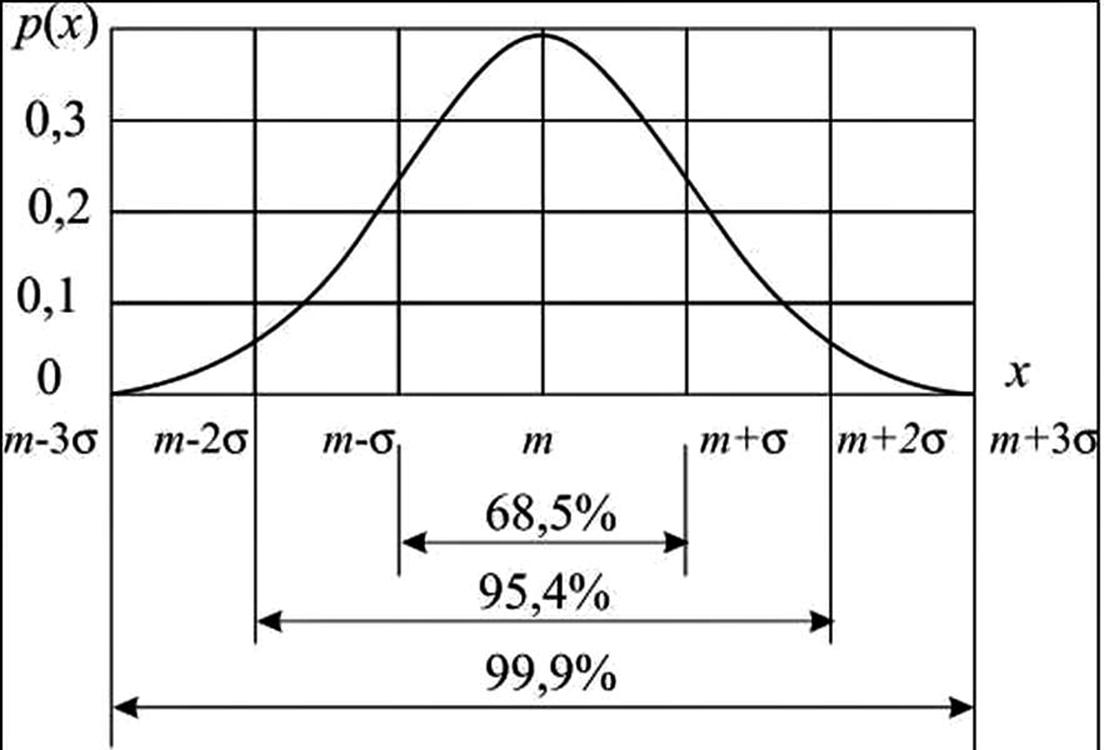
По большому счёту, к этому распределению должно стремиться любое управление. Так это основа биологии жизни. То есть, в нормальных условиях в жизни любого вида исходя из законов Эфироворота и для нас более понятных от шести объективных закономерностей,

Всегда имеют быть определенные уровни быстрой смертности и сверх долгого жития, но в среднем основная численность имеет вид нормального распределения. По сути, есть те, кто не доживает и 5 лет, а есть те, которые живут 90 лет и более. Но в среднем на современном этапе большинство людей живут от 60 до 70 лет.

Точно так же, как и в дискретном распределении и в непрерывном распределении существуют математически вычисляемые основные параметры в виде числовых характеристик случайных величин.

То есть, присутствует и математическое ожидание и дисперсия и так далее. Произведя расчёт которых в очень простом виде для тех кто может пользоваться Microsoft Excel, и соотнеся их результат с подобными процессами можно выявить разные тенденции прохождения различных процессов, которыми мы хотим или уже управляем.

Перечислим их по порядку только те, которые определяются другим способом.

1. Математическое ожидание.

Определяется с помощью интегрирования, функции плотности распределения вероятностей.

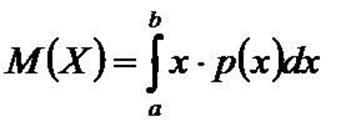
3. Дисперсия.

Дисперсия непрерывной случайной величины X, возможные значения которой принадлежат всей оси Ох определяется равенством:

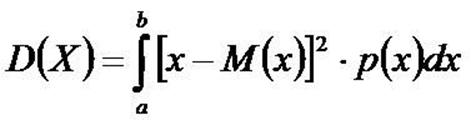
4. Медиана.

Медиана (μ) – значение случайной величины, для которого вероятность того, что СВ не превзойдет это значение, равна 0,5 (площадь под кривой распределения плотности вероятности делит пополам.

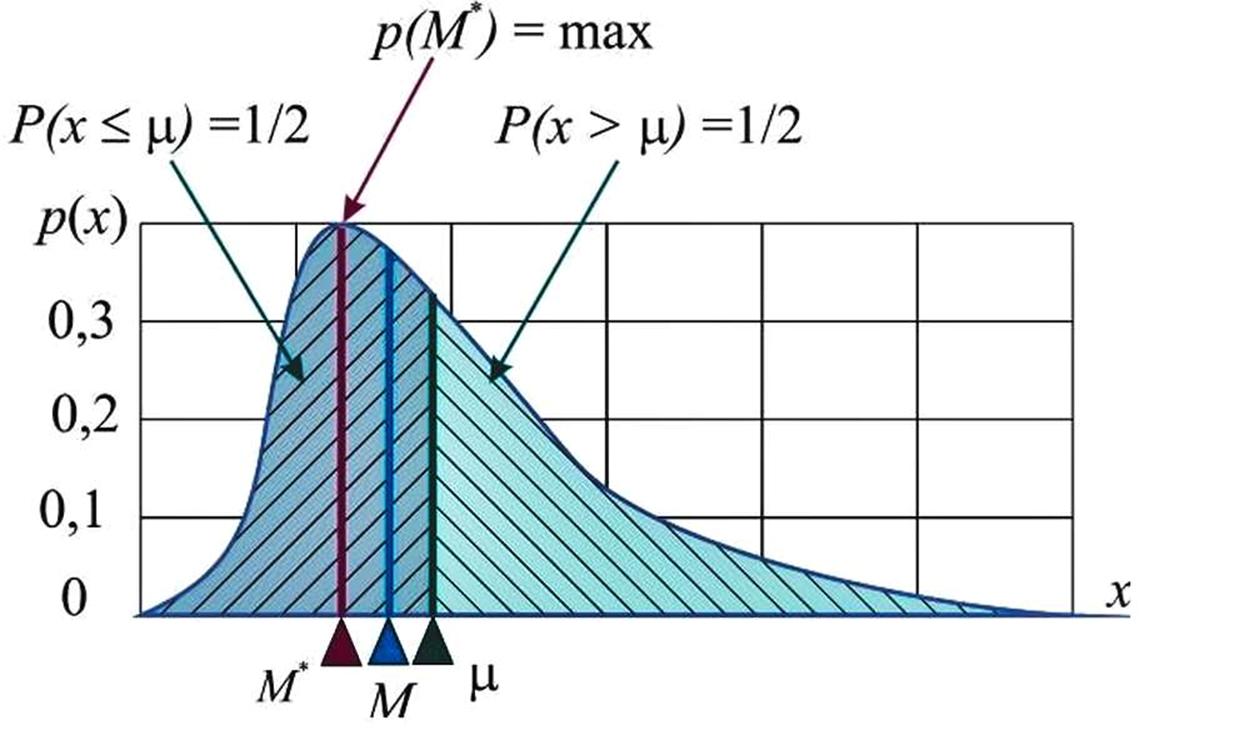
Где М* это Мода. Модой непрерывной случайной величины X называется точка X, в которой плотность f(x) достигает своего максимума, а М это математическое ожидание.

Небольшое обобщение.

Если очень коротко, то собираем все дискретные данные, строим графики и вычисляем необходимое для управления. Потом собираем дополнительную информацию, и информацию как меняются вычисленные ранее значения относительно времени. То есть к примеру, через час или через неделю, через 10 лет, в зависимости от процесса.

По сути это уже будут непрерывные СВ. Из всего этого формируем функции распределения СВ и плотности распределения СВ. Производим необходимые расчёты для простоты соотношений. После чего уже делаем соответствующие выводы и принимаем соответствующие решения.

После того как вы немного разобрались с главной сутью графиков распределения случайных величин, обратимся ещё раз к наилучшему варианту представления статистических данных.

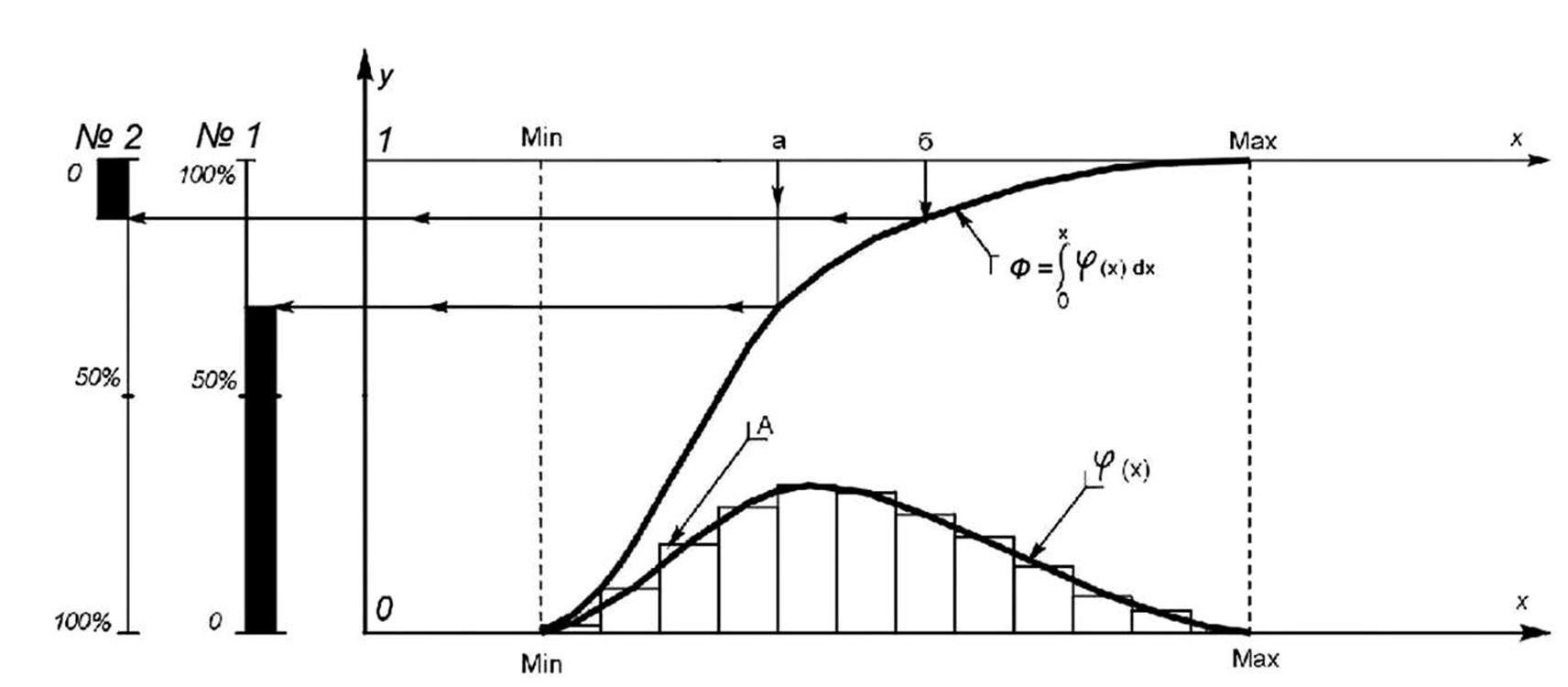
На рисунке показана система координат 0xy:

* По горизонтали — ось абсцисс x. По оси x откладываются значения параметра, по которому распределено рассматриваемое множество.

* По вертикали — ось ординат y. По оси y откладываются значения функций плотности распределения φ(x) и интегральной функции распределения Ф(x).

Параллельно оси абсцисс на уровне максимально возможного значения интегральной функции распределения y = Ф(x) = 1 проведена горизонтальная шкала, дублирующая ось x. Она может быть полезной (для удобства) в некоторых случаях при работе со статистическими данными, представленными в такой графической форме.

Кроме того, параллельно оси y размещены ещё две шкалы: № 1, № 2.

Обе эти шкалы — процентные, но встречной направленности, поскольку в одних задачах необходим отсчёт доли статистики, включающей в себя максимум значения рассматриваемого параметра; а в других задачах необходим отсчёт доли статистики, включающей в себя минимум значения рассматриваемого параметра. Как ими пользоваться, видно из самого рисунка:

* Широкая чёрная полоса вдоль шкалы № 1 отмечает долю статистики, в которой значение анализируемого параметра меньше, чем значение «а», отмеченное на верхней шкале изменений аргумента.

* Широкая чёрная полоса вдоль шкалы № 2 отмечает долю статистики, в которой значение анализируемого параметра выше, чем значение «б», отмеченное на верхней шкале изменений аргумента.

Кроме того, в осях 0xy показаны:

* Столбиковая диаграмма «А». Высота каждого столбика в масштабе оси y равна доле статистики, попадающей в диапазон значений аргумента x, который лежит в основании каждого из столбцов.

* Если сделать более мелкое разделение диапазонов, то дискретная плотность распределения «А» может быть аппроксимирована непрерывной плотностью распределения φ(x), что в ряде задач может быть более удобным.

* Если плотность распределения φ(x) существует (в жизни встречаются распределения, для которых функция плотности распределения не существует) и её проинтегрировать, то получим кривую Ф(x), с масштабом отображения которой по оси y связаны шкалы № 1 и № 2.

* Дискретный аналог кривой Ф(x) не показан, чтобы не загромождать рисунок. Его можно получить, если к высоте каждого из столбиков диаграммы «А» добавить сумму высот всех столбиков, находящихся слева от него по оси x.

* Кривая Ф(x) (и её не построенный дискретный аналог) вместе со шкалами № 1 и № 2 показывает статистическое распределение анализируемого множества по рассматриваемому параметру x.

Представление в такой форме разного рода статистик (в том числе и нескольких статистик в одних и тех же осях) представляется наиболее удобным.

Если в этой форме представлена социальная статистика, то в осях 0xy единицей измерения численности населения в разных статистических группах является общая численность населения: в масштабе оси y она равна 1. А каждая выделенная социальная группа, на которую приходится некая доля статистического распределения по рассматриваемому параметру x, — доля от этой единицы. Шкалы № 1, и № 2 по своей смысловой нагрузке аналогичны оси y, с тою лишь разницей, что они оразмерены в более предпочтительной для многих людей процентной мере.

Горизонтальные шкалы аргумента x могут быть как размерными, так и обезразмеренными по тем или иным характеристическим показателям, которые характерны для той или иной теории подобия привлекаемой к анализу и проектированию статистических характеристик соответствующего объекта (системы).

В этой форме может быть отображена любая по содержанию статистика, из некоторого набора статистик, которыми может характеризоваться любое управление и взаимодействия с природной средой.

***

Важное практическое задание.
Для лучшего уяснения сути, вам необходимо вспомнить, что такое Опорный Сигнал, смотрим главу /3.9.15.1. Алгоритм 1/. И попытаться преобразовать уже понятный нам рисунок функции и плотности распределения, в графический опорный сигнал.

То есть, попробуйте сделать такой Опорный Сигнал, чтобы с первого взгляда была понятна суть выше указанного рисунка, к примеру, как рисунок с картинками лиц в Методе Динамического программирования в главе /7.3.8. Метод динамического программирования/, эту главу мы будем разбирать далее, но нет ничего страшного, если вы немного забежите вперёд и посмотрите этот рисунок.
Проявите фантазию и творчество и создайте свой Опорный Сигнал, это поможет вам окончательно разобраться с этим вопросом и потом очень легко его пояснить другим людям. При этом, возможно именно ваш вариант разлетится в Интеренете и поможет всем нам быстрее перешагнуть статистическую безграмотность, поголовно процветающую у нас.

***

Теперь необходимо немного пояснить вопрос, с которым мы столкнёмся позже, но который без понимания вероятности наступления того или иного события понять будет затруднительно.

Именно от понимания этого вопроса и зависит осознание термина – качество управления.

Вероятностная предопределённость осуществления события – равна “математической вероятности самоосуществления” события, умноженной на личность управленца, как носителя определённых возможностей.

Или в другом соотношении.

Под мерой необходимости управления можно ещё понимать уровень и качество управления как профессионализм управленца.
Вероятность самоосуществления определенного варианта это, по сути, вероятность того, что без всякого управления этот вариант как бы разрешится сам. В принципе уровень этого показателя можно понять из сравнения двух процессов – управление поездом и машиной в том смысле как надо уметь именно рулить. То есть, если рулить при езде на машине, то уровень и вероятность будет очень мала без всякого управления, куда-либо доехать. А вот рулить поездом вообще не надо, тонны железа сами по рельсам хорошо и ровно катятся и, следовательно, вероятность осуществления события в смысле доехать до цели в этом случае будет довольно высока. Здесь так же надо иметь в виду факт осуществления этого варианта вообще. А вот здесь как раз без статистик и теории вероятности будет что-либо определить довольно проблематично. То есть, оценку объективно возможного осуществления того или иного события можно осуществить исключительно из анализа статистик, из опыта и математически подтвержденных данных исходя из подобия ранее происходивших событий. По сути, если не умеешь, или нет возможности полноценно собирать статистические данные, их анализировать и просчитывать вероятности, то нет и возможности оценить меру необходимого профессионализма управленца и уровень его качества последующего управления.

По большому счету, используя эту формулу можно не только просчитать необходимый профессиональный уровень управленца для уже знакомого процесса, но также можно впоследствии и оценить уровень управления и его качество по его завершению и даже спрогнозировать что надо для лучшего управления.

К примеру, возьмём за неизвестный Х, то, что это искомое качество управления некого процесса. Вероятность самоосуществления события допустим, у нас будет 0,9 (не надо рулить поездом). В числителе будет у нас вместо единицы стоять некий показатель совокупный статистический показатель, который буде от 1 до 0, характеризовать уровень достижения цели. К примеру, если всё нормально и достигли пункта назначения в более или менее приемлемом виде, то значение будет чуть меньше единицы, к примеру, 0,9 неких единиц.

А если очень сильно опоздали и ещё были другие статистики, ухудшающие общий показатель, то естественно, к примеру, будет результат в 0,2 единицы.

1 вариант Х = 0,9/0,9 = 1 (по сути 1 это 100%, следовательно, управление было на высоте)

2 вариант Х = 0,2/0,9 = 0,22 (по сути 0,22 это 22%, следовательно, управление было, мягко говоря, плохим и уровень компетентности и профессионализма управленца очень низок так как даже при вероятности 0,9 он не смог справится и даже не только не справился, а наоборот мешал и вредил).

Как пример – наилучшим управлением в обществе будет считаться управление, при котором устойчиво снижаются цены на удовлетворение демографически обусловленных потребностей для всех граждан такого общества. То есть, надо в числитель занести обобщенный коэффициент, который бы отражал статистику изменения цен именно на эти потребности. И тогда можно легко оценить качество управления президента, правительства, местных органов власти и так далее.

См. ролик в рекомендуемых видео:

/ 7185_Вероятностная предопределенность/

Практические Дополнения.

Для пояснения всего вышесказанного приведём совсем немного примеров использования того, о чём говорилось ранее. Хочется сказать, что это только мизерная часть, затрагивающая очень малую область возможного применения теории вероятности и статистики.

Статистика как таковая и теория вероятности и навыки с ними работы необходимы любому управленцу для адекватного выявления факторов среды, которые давят, для правильного определения вектора целей и выявления основных параметров контроля и управления. К тому же без выше указанного, банально невозможно полноценно запустить режим управления в формате Предиктор - Корректор.

Пример № 1

Некий студент выучил 25 экзаменационных вопросов из 60. Какова вероятность для него сдать экзамен, если для этого необходимо положительно ответить не менее чем на два из трёх вопросов?

В результат мы получили вероятность 37 %, это результат, даже не дотягивает до классического варианта принятия решения в 51 %. Когда преодолён рубеж между «да» и «нет», «плохо» и «хорошо», «сдал» или «не сдал».

То есть, чтобы хоть как-то приблизиться к наилучшему варианту исхода события, студенту необходимо ещё выучить несколько билетов, иначе беда неминуема, и на это ему указывает даже теория вероятности.

Пример № 2

Этот пример показывает как исходя из необходимых знаний, управленец должен принять то, или иное решение. Или лучше сказать, выбрать ту или иную гипотезу о необходимости тех или иных действий сейчас и в будущем, дабы была достигнута цель с наименьшими потерями. Если управленец не будет владеть такими необходимыми знаниями, а решение всё же надо принять, то естественно есть вероятность, что он может принять не правильное решение.

Так вот, чтобы снизить эту вероятность и необходимо всё, о чём идёт речь в этом разделе знать каждому управленцу.

Допустим, для нормального технологического процесса нужна температура 250 градусов. Для проверки этого, 5 раз измерили температуру и получили 256 градусов. Из ранее предыдущих опытов известно, что среднеквадратическая погрешность измерений составляет 6 градусов. Эта погрешность может складываться от погрешности термометра, от случайных различных обстоятельств проверки и т. д.

Решение

Ещё раз обратим внимание – что означает «на уровне значимости 0,05»?

Это означает, что с вероятностью 5% мы убрали правильную гипотезу.

Здесь остаётся взвесить риск – насколько критично чуть-чуть уменьшить температуру (если мы всё-таки ошиблись и температура на самом деле в норме).

Если даже небольшое уменьшение температуры недопустимо, то имеет смысл провести повторное, более качественное исследование: увеличить количество замеров (n), использовать более совершенный термометр, улучшить условия эксперимента и т. д.

Пример № 3

Пример № 4.

Навык умения использовать, теорию вероятности и методы математического анализа и статистики особенно необходимы при условиях, когда надо выбрать один лучший вариант из нескольких направлений или когда необходимо отслеживать несколько направлений одновременно. Особенно это необходимо при сетевом планировании и создании сложных схем структурного управления и создания технических заданий для реализации Искусственного Интеллекта (ИИ) и машинного обучения (МО). По сути, этот аспект очень важен для структурного управления, в который входят множественные параметры, которые изначально можно отдать на отработку заранее отлаженных алгоритмов в электронно-вычислительной технике. К тому же именно здесь стоит обратить особое внимание на строй психики программистов, так если у них Воля не подчинена диктатуре Совести, то любое ваше управление будет завесить именно от этого. Следовательно, избежать катастрофических ошибок будет крайне тяжело, даже если вы будете прилагать множественные усилия по праведному управлению.

А сейчас приведём пример.

Две грузовые машины должны приехать на разгрузку в промежуток времени от 19. 00 до 20. 30. Разгрузка первой машины идёт 10 минут, второй машины идёт – 15 минут. Какова вероятность того, что одной машине придется ждать окончания разгрузки другой?

Итак, во-первых, машины могут подойти на разгрузку в любом порядке, во-вторых – в любые моменты времени в течение полутора часов.

С первого взгляда решение представляется довольно тяжёлым. И для необразованного человека оно действительно будет «не по зубам».

Решение сначала выясняем длительность временнОго промежутка, на котором может состояться встреча. В данном случае это 90 минут. На первом шаге изобразим прямоугольную систему координат, где в подходящем масштабе построим квадрат размером 90 на 90 единиц. При этом одна из вершин квадрата совпадает с началом координат, а его смежные стороны лежат на координатных осях.

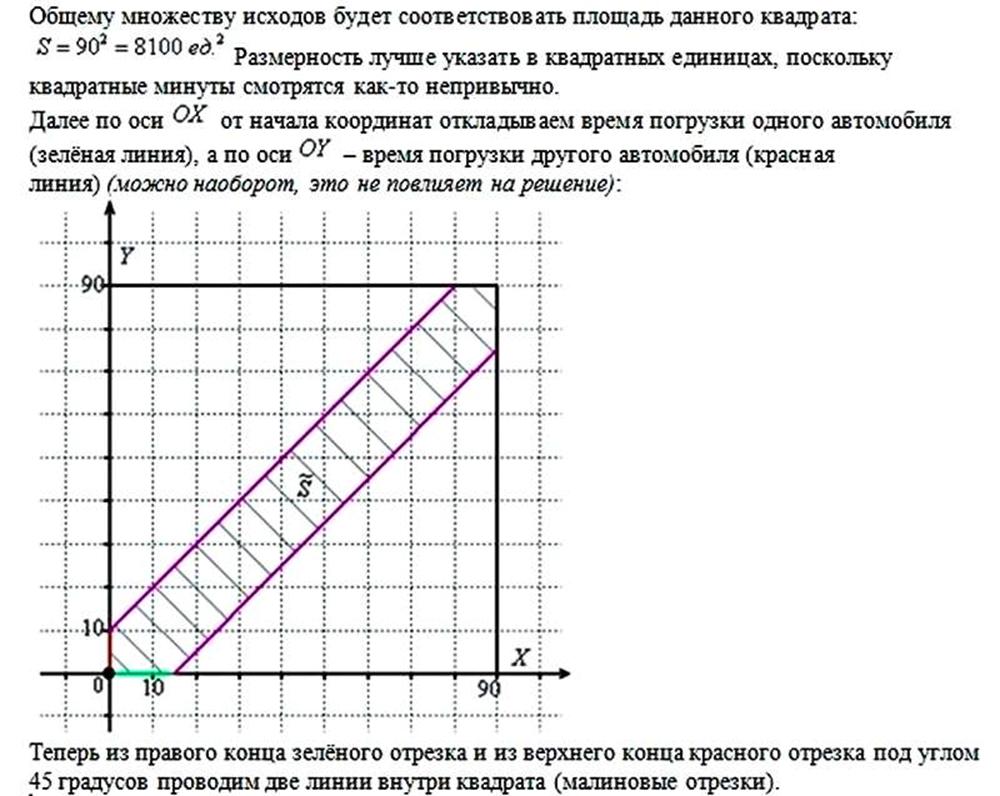
По сути если вы знаете этот простейший прием, то вам не составит труда создать приемлемый график любой логистической операции. То есть, у вас не будет возможных простоев и задержек от, казалось бы, случайных стечений обстоятельств.

Если управленец адекватный и ведёт историю своего управления, дотошно ведёт статистику главных параметров управления, как по количественным характеристикам, так и качественным. То по большому счёту, такой управленец имеет базу данных, которую он может инструментами теории вероятности проанализировать. Из полученных результатов он может синтезировать критерии, благодаря которым, к примеру, зная законы распределения вероятностей по уже знакомым процессам, он сможет смоделировать подобный процесс, но с которым он ранее не встречался. По сути, он получает возможность качественно прогнозировать по подобию и тем самым запускать именно наилучшую схему управления в режиме «Предиктор-Корректор».

Пример № 5.

Теория вероятности очень наглядно используется во многих областях управления.

К примеру:

вероятность банкротства (антикризисное управление)
управление рисками (финансовый менеджмент)
вероятность внедрения новых технологий (инновационный менеджмент)
оценка непредвиденных затрат (операционный менеджмент)

По сути, теория вероятности исследует закономерности в случайных явлениях. Под случайными явлениями понимают явления, исход которых предугадать невозможно.

Оценка вероятности банкротства

Индекс (пятифакторная модель) Альтмана: Z = 1,2 * Коб + 1,4 * Кнп + 3,3* Кр + 0,6 *Кп+ 1,0* Ком

Коб — доля оборотных средств в активах, т. е. отношение текущих активов к общей сумме активов;

Кнп — рентабельность активов, исчисленная исходя из нераспределенной прибыли, т. е. отношение нераспределенной прибыли к общей сумме активов;

Кр — рентабельность активов, исчисленная по балансовой стоимости (т. е. отношение прибыли до уплаты % к сумме активов;

Кп — коэффициент покрытия по рыночной стоимости собственного капитала, т. е. отношение рыночной стоимости акционерного капитала к краткосрочным обязательствам.

Ком — отдача всех активов, т. е. отношение выручки от реализации к общей сумме активов.

если Z < 1,81 – вероятность банкротства составляет от 80 до 100%;
если 2,77 <= Z < 1,81 – средняя вероятность краха компании от 35 до 50%;
если 2,99 < Z < 2,77 – вероятность банкротства не велика от 15 до 20%;
если Z <= 2,99 – ситуация на предприятии стабильна, риск неплатежеспособности в течении ближайших двух лет крайне мал.

Управление рисками.

Пример: Имеются два варианта вложения капитала. Установлено, что при вложении капитала в мероприятие А получение прибыли в сумме 15 тыс. руб. — вероятность 0,6; в мероприятие Б получение прибыли в сумме 20 тыс. руб. — вероятность 0,4. Тогда ожидаемое получение прибыли от вложения капитала (т. е. математическое ожидание) составит:

по мероприятию А 15 • 0,6 = 9 тыс. руб. ;
по мероприятию Б 20 • 0,4 = 8 тыс. руб.

Здесь мы видим, что если не учитывать вероятность, то можно поддаться более высокой начальной прибыли в 20 тыс. рублей и принять ошибочное решение. Именно вероятность 0,6, которая выходит исходя из множества сторонних данных, которые можно взять из прежнего опыта и соответствующей выборке и даёт управленцу громадное преимущество при принятии решения.

Пример № 6

Если не знать ничего по теории вероятности и мат. анализу в смысле пониманиям даже по минимуму о функции распределения случайной величины и плотности распределения случайной величины, то можно любых «баранов» кормить данными средней статистики.

При этом, только понимая нижеуказанные графики, всё сразу встаёт на свои места в смысле того, что сразу видно ужасающая несправедливость большинства трудового народа.

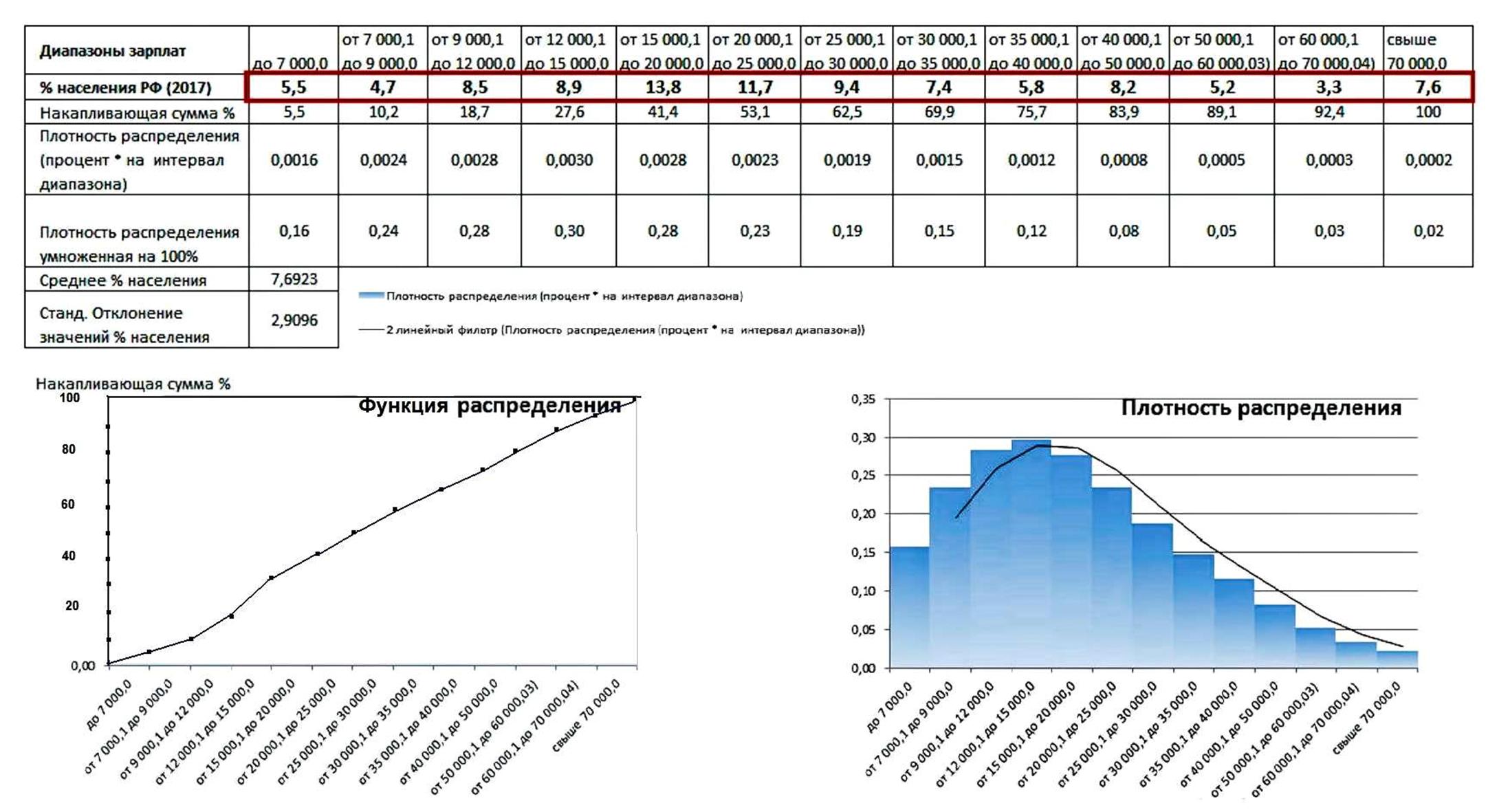
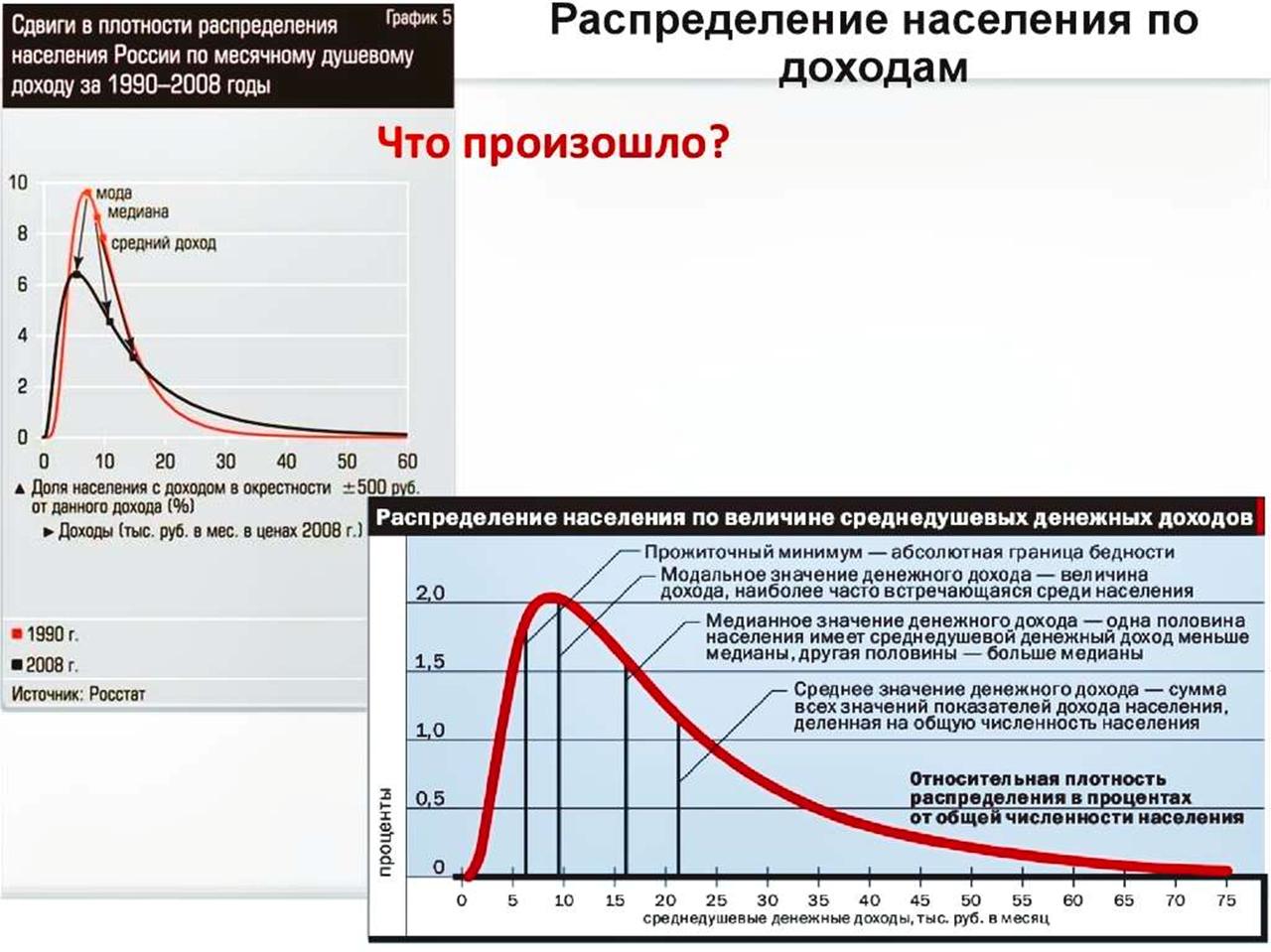
Из графиков видно, что медианное значение исходя из своей сути, которая находится по спец формулам указывает из графика на то, что больше половины населения имели доходы около 16000 хотя по стране все кричат о среднем в 22000.

В зоне ниже прожиточного минимума, то есть, банально нищибродствуют и голодают более 15 процентов населения и в основном, у которых есть дети. И это в той стране, в которой ещё 30 лет назад не было ни голодных, ни нищих, как по определению, так и фактически вообще.

И если сводить и показывать такие простые графики раз в 5 лет перед выборами в разные органы управления, то можно реально и очень просто видеть, как в динамике отражаются те факторы, которые явно показывают качество жизни большинства людей.

Следовательно, они отражают и качество управленцев, которые были у руля власти за это время.

Такие наглядные результаты знаний теории вероятности и статистики доступны любому школьнику. И поэтому если действительно люди хотят изменить свою жизнь к лучшему. То каждый взрослый и каждый ребенок, достигший возраста совершеннолетия, должен в лёгкую всем этим пользоваться. И тогда он сможет всегда принять компетентное решение, как в любом управлении, так и при любом, так сказать, своём волеизъявлении на выборах. Дабы, в органы управления, не смогли пройти бездарные неучи, а если бы и проникли, то через аппарат статистики их дурь и некомпетентность была бы вскоре обнаружена и была бы понятна каждому нормальному гражданину и человеку.

Небольшое замечание.

При получении и выборке всех необходимых значений и данных для управления и последующей их обработке, необходимо сразу убирать те, которые явно не входят в рамки привычного и разумного (ошибка сбора). То есть, надо отсеивать те данные, которые явно отличаются от подобно многократно получаемых данных ранее. Следовательно, надо стараться делать выборку внимательно из наиболее возможного количества единиц, но естественно всё в рамках разумного. По сути, ряд собранных данных должен быть достаточным и близким к области допустимых параметров.

Хочется ещё раз сказать, что теория вероятности и основы математической статистики необходимы любому управленцу, а управление это неотъемлемая часть любого человека. Поэтому, по сути, все эти знания и навыки нужны абсолютно каждому.

Любое управление начинается с выбора и сбора необходимых статистических данных, с выбора параметров которые давят на человека, с выбора управляемых данных и контрольных. После чего их надо проанализировать, сделать выводы, выбрать главные и второстепенные, выявить тенденции и различные соотношения. Только после этого, можно уже принимать какое – либо решение.

К примеру, как поступают в медицине. Дабы поставить диагноз надо совершить опрос пациента, взять базовые химические и другие анализы. Потом полученные данные совместить с опытом и имеющимися аналогиями, высказать предположение и дать рекомендации. Через некоторое время опять всё провести заново и полученные результаты сравнить с прошлыми осмотрами. По сути, всё это статистика и вероятность. Это всё довольно несложная наука, но её методы настолько улучшают качество любой деятельности, что если всё это игнорировать, то нет никой возможности делать что-либо хорошо и на продолжительном отрезке времени однозначно.

Стоит ещё раз сказать, что когда вы имеет перед собой любых, два варианта для принятия решения, вам в обязательном порядке необходимо просчитать вероятность наступления каждого. И если одно из направлений будет иметь значение хотя бы 51 % (0,51), то выбор этого варианта в долгосрочной перспективе обязательно приведёт к успеху.

Да, на кротком промежутке времени, может быть иное, но как говорится, нам спешить некуда. Ведь мы хотим жить долго и счастливо. Так что, всегда считаем вероятности и выбираем большую вероятность и делаем всё, чтобы она осуществилась.

По сути, вы в этом случае становитесь владельцем казино своей жизни, где вы всегда будете в выигрыше.

Главная задача для всех нас на будущее, это снабдить имеющуюся теорию вероятности, адекватными примерами из жизни, с которыми могут сталкиваться все люди по своей жизни.

Сейчас, и в прошлом, теорию вероятности и мат. статистику изучают и изучали миллионы студентов, а, по сути, они и не знают её, и применять её не могут. Всё делается ради получения зачёта и экзамена. Всё это бесполезно и бессмысленно.

Хотя главная суть и необходимые навыки катастрофически нужны каждому человеку.

Так что, давайте всем нашим Русским Миром наделим имеющуюся теорию надлежащими практическими формами, набив на которых руку, любой человек сможет стать адекватным управленцем в любой области и в том числе своей жизни и жизни общества, в котором он живёт. То есть, нужны примеры, задачи и их решения в наглядных простых формах, пройдя которые любой человек может получить необходимый навык, который можно применять в жизни.

По сути, все, что было указано выше и в уроках, которые рекомендуются ниже, в последствии, надо перевести на реальные примеры из жизни под ракурсом ДОТУ. То есть, надо Теорию Вероятности и Мат. Статистику учить на реальных примерах использования в управлении по ПФУ.

Вот именно эта задача для Вас, для нового поколения.

По большому счёту, надо собрать некую базу примеров, решая и проходя которые, человек не только осваивает основы этих дисциплин, но и нарабатывает специализированные алгоритмы в подсознании и опыт, с навыком для реального управления на практике. Именно разрешая простейшие житейские примеры, с учётом всего вышесказанного, будет не простая учёба и заучивание формул, а приобретение именно автоматического навыка использования их в жизни.

Примечание.

Основой для организации бесструктурного управления являются знания математического анализа и теории вероятности. Если очень грубо, то если ты это знаешь, значит, можешь управлять толпой.
См. ролик /7181_Бесструктурное управление примеры/

См. дополнительные пояснения.

Интернет:

Для быстрого входа в тему и получения стандартных и устойчивых знаний смотри сайт

http://www.mathprofi.ru

Проходи все уроки по Теории Вероятности и Математической Статистики, всё рассказано доступным языком для среднего школьника.

К тому же не помешает разобраться:

Лимиты.

http://www.mathprofi.ru/predely_primery_reshenii.html

Производные

http://www.mathprofi.ru/opredelenie_proizvodnoi_smysl_proizvodnoi.html

Интегралы

http://www.mathprofi.ru/chto_takoe_integral_teorija_dlja_chainikov.html

Если к сайту нет доступа, то смотри в рекомендуемой литературе:
/718_Презентация по терверу/
/719_Уроки по матстату/
/720_Уроки по терверу/

и в рекомендуемых видео:

/с 7194 по 7207/ - К урокам по статистики

Литература:

/ 743_Вероятность и предсказание как наука/

/ 795_Размышления о вероятностях/

/ 7106_Стандартизация как управление/

/ 716_Как манипулируют неучи статистикой/

Видео:

/7185_Вероятностная предопределенность/

/751_Личность и вероятностная предопределенность/

/731_Два слова о Статистике/

/7250_Два слова о вероятности/

/3128_Визуализация производной и мат.анализа_круто/

/7291_Зачем матстат и тервер коротко/

Следующая страница ➤

Данилёнок Вадим Евгеньевич
С этого места Вы можете бесплатно скачать книгу по материалам сайта и выразить благодарность автору по указанной ссылке
СКАЧАТЬ КНИГУ БЕСПЛАТНО
или нажав на верхнюю картинку

* * * * * * * * *